algorithm

[TOC]

查找

顺序查找

1. 就是普通的查找方法

      
   int search(int arr[],int length,int targetElement){
       for (int i = 0; i < length; ++i) {
           if(targetElement==arr[i]){
               return i;
           }
       }
       return -1;
   }
      
   //修改过后的代码
   int searchPlus(int arr[],int length,int targetElement){
       int n=length-1;
       while(arr[n]!=targetElement&&n>-1){
           n--;
       }
       return n;
   }
      

折中查找

1. 折中查找

     int main(){
       int nums[10]={1,2,3,4,5,6,7,8,9,10};
       int left=0;
       int right=sizeof(nums)/sizeof(int)-1;
       int mid=(left+right)/2;
       while(left<=right){
           if(nums[mid]>6){
               right=mid+1;
           }else if(nums[mid]<6) {
               left=mid-1;
           }else {
               printf("find it: %d",nums[mid]);
               break;
           }
           mid=(left+right)/2;
       }
       return 0;
   }
      

2. 按比例查找（差值查找）

   这个算法是根据这种算法来的，只是采用的比例不是1/2

   这个算法可以用于大型的增长相对来说有序的线性表

3. 斐波那契查找

   根据的还是折半查找，只不过这个的表是斐波那契数列

4. 线性索引查找

   • 索引方式

     • 稠密索引

       适用于数据量不大

       

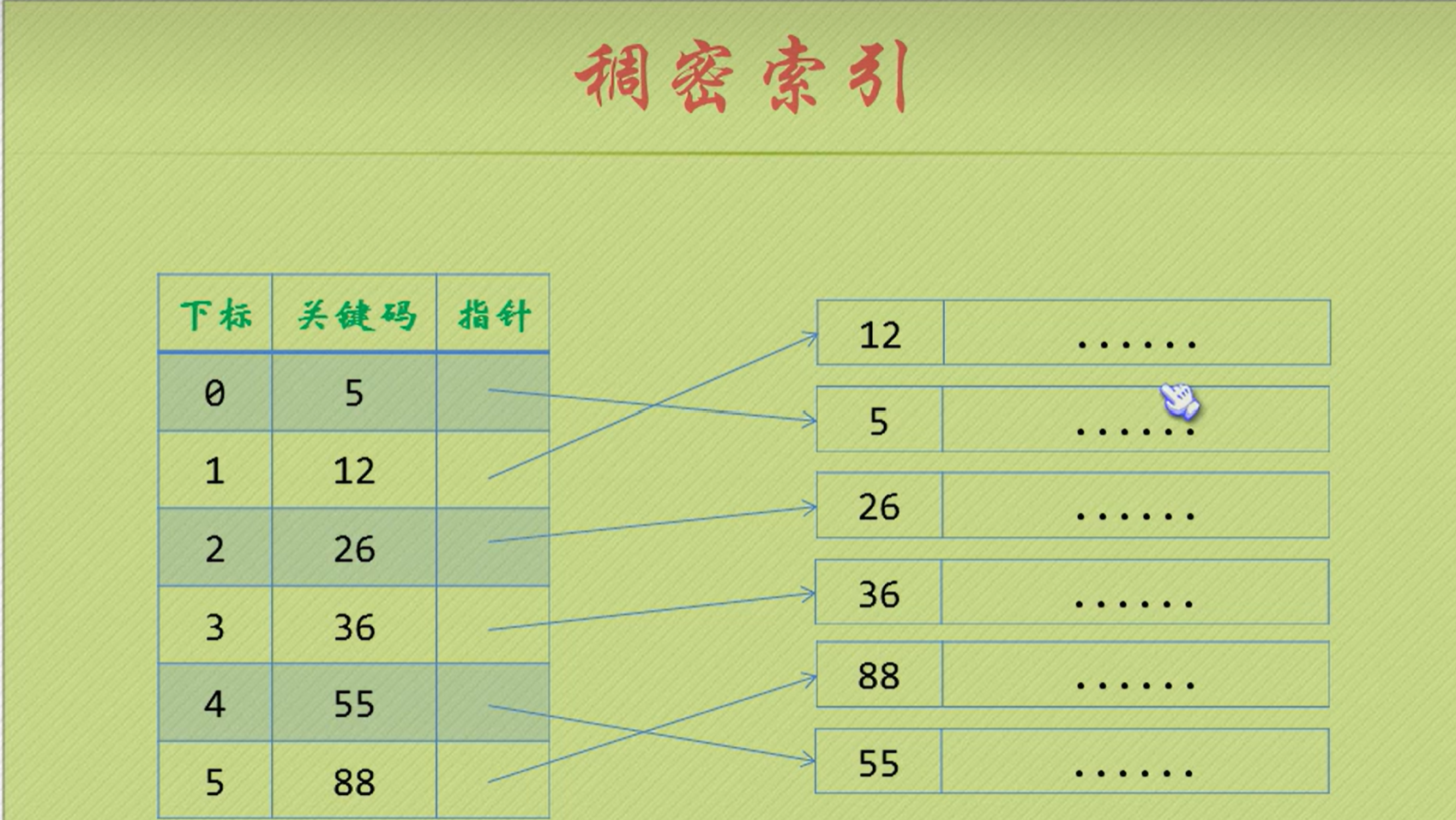
     • 分块索引

       

     • 倒排索引

       

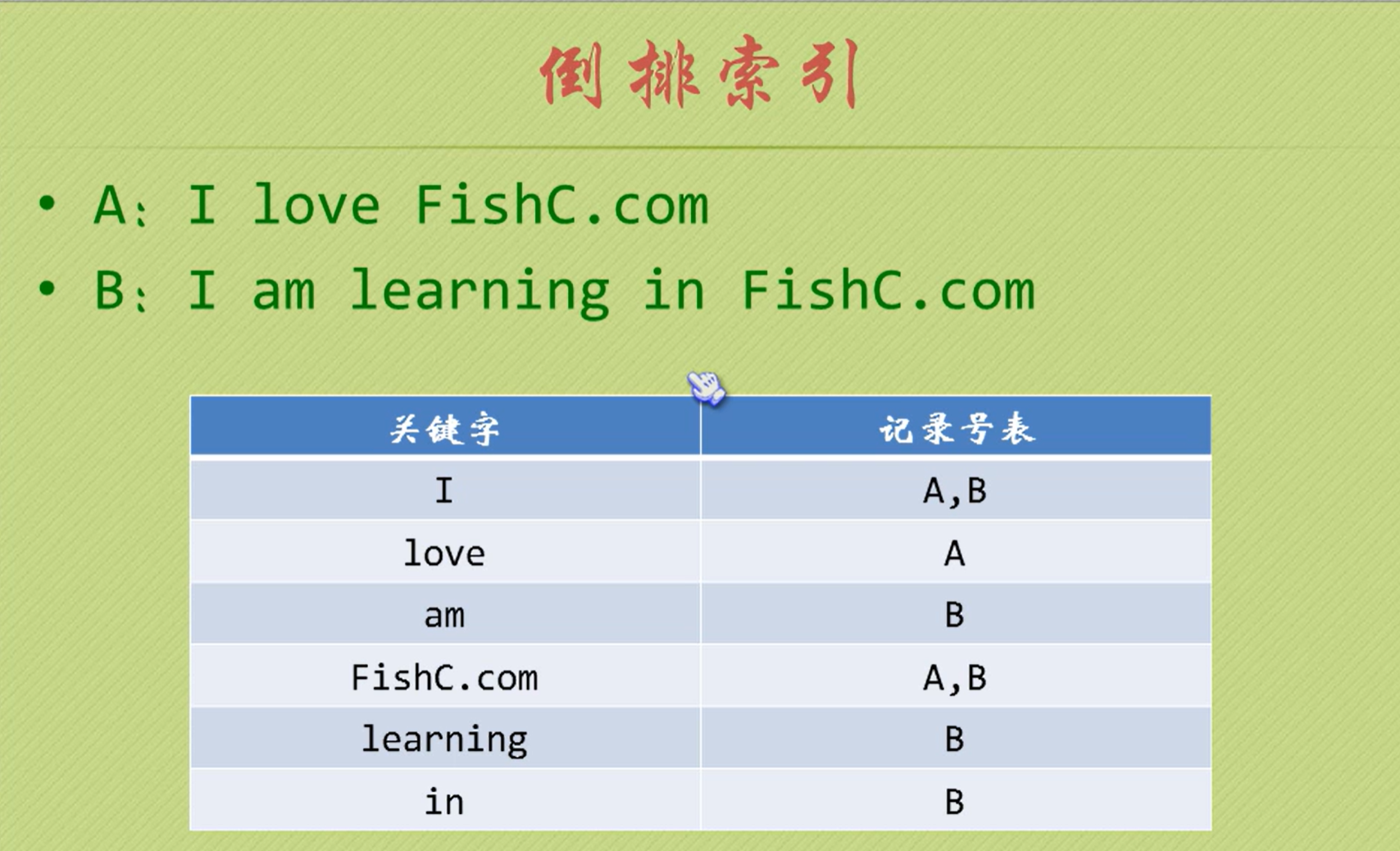
二叉排序树（二叉查找树）、

没有学会

下面代码有bug

#include <malloc.h>
#include "math.h"
#include "stdio.h"
#include <string.h>

#define size 9

typedef struct Node {
    struct Node *pLeft;
    struct Node *pRight;
    int value;
} Node, *pNode;

int sub = 0;

int nums[size] = {0};


void insertNode(pNode *pRoot, int val) {
    if (*pRoot == NULL) {
        *pRoot = (pNode) malloc(sizeof(Node));
        (*pRoot)->value = nums[sub];
        (*pRoot)->pLeft = NULL;
        (*pRoot)->pRight = NULL;
        return;
    }
    if ((*pRoot)->value > nums[sub]) {
        insertNode(&(*pRoot)->pLeft, val);
    } else if ((*pRoot)->value < nums[sub]) {
        insertNode(&(*pRoot)->pRight, val);
    } else {
        sub++;
        return;
    }
}


void createTree(pNode *pRoot) {
    for (; sub < size; sub++) {
        insertNode(pRoot, nums[sub]);
    }
}

void destroyTree(pNode *pRoot) {
    if ((*pRoot)->pLeft != NULL) {
        destroyTree(&(*pRoot)->pLeft);
    }
    printf("  %d  ", (*pRoot)->value);
    if ((*pRoot)->pRight != NULL) {
        destroyTree(&(*pRoot)->pRight);
    }
    free(*pRoot);
}

//查找二叉树的元素
int SearchBSF(pNode *root, pNode *value, int val) {
    /*
     * explain:查找二叉树
     * return:value,如果存在，就返回此节点的地址，否则返回上一个节点的地址
     */
    //如果发现了值，就直接返回
    if ((*root)->value >= val) {
        *value = *root;
    }
    if ((*root)->value == val) {
        return 1;
    }
    if ((*root)->pLeft != NULL) {
        int i = SearchBSF(&(*root)->pLeft, value, val);
        //如果不写if,可能会出现后面还没有遍历，前面就已经退出
        if (i == 1) {
            return i;
        }
    }
    if ((*root)->pRight != NULL) {
        int i = SearchBSF(&(*root)->pRight, value, val);
        if (i == 1) {
            return i;
        }
    }
    return 0;
}

//插入操作
int InsertBST(pNode *root, int val) {
    /*
     * explain: 对二叉树排序树进行插入操作
     */
    pNode value = NULL;
    if (!SearchBSF(root, &value, val)) {
        pNode tem = (pNode) malloc(sizeof(Node));
        if(tem==NULL){
            return 0;
        }
        tem->value = val;
        tem->pRight = NULL;
        tem->pLeft = NULL;

        if (value->value > val) {
            tem->pLeft = value->pLeft;
            value->pLeft = tem;
            return 1;
        } else if (value->value < val) {
            tem->pRight=value->pRight;
            value->pRight=tem;
            return 1;
        }
    } else {
        printf("insert error");
    }
    return 0;
}

int delete(pNode* p){
    pNode q,s;
    if((*p)->pRight==NULL){
        q=*p;
        (*p)=(*p)->pRight;
        free(q);
        q=NULL;
    }else if((*p)->pLeft!=NULL){
        q=*p;
        (*p)=(*p)->pLeft;
        free(q);
        q=NULL;
    }else{
        q=*p;
        s=q->pRight;
        while(s!=NULL){
            q=s;
            s=s->pRight;
        }

        if(q==*p){
            q=s;
            s=s->pLeft;
            (*p)->value=q->value;
            free(q);
            q=NULL;
            (*p)->pLeft=s;
        }else{
            (*p)->value=s->value;
            q->pRight=s->pLeft;
            free(s);
            s=NULL;
        }
    }
    return 1;
}


//删除节点
int deleteBST(pNode* root,int val){
    pNode tem;
    if(*root==NULL) {
        printf("don't have tree");
    }else {
        if(SearchBSF(root,&tem,val)){
            return delete(&tem);
        }
    }
    return 0;
}



int main() {
    pNode root = NULL;
    pNode valueTem = NULL;
    int value;
    for (int i = 0; i < size; ++i) {
        scanf("%d", &nums[i]);
    }
    printf("input value: ");
    scanf("%d", &value);
    createTree(&root);
    if (SearchBSF(&root, &valueTem, value)) {
        printf("hava value %d\n", value);
    } else {
        printf("don't hava value\n");
    }
    printf("value node is:%d\n", valueTem->value);
    InsertBST(&root,value);
    if (SearchBSF(&root, &valueTem, value)) {
        printf("hava value %d\n", value);
    } else {
        printf("don't hava value\n");
    }
    deleteBST(&root,value);
    destroyTree(&root);
    return 0;
}

平衡二叉排序树(AVL树)

1. 定义

   左右子树的高度之差的绝对值小于等于1

   左右子树是一个平衡二叉排序树

2. 平衡因子

   左右子树的高度差(左子树-右子树)

   -1,1,0

3. 调整平衡二叉树

   

   

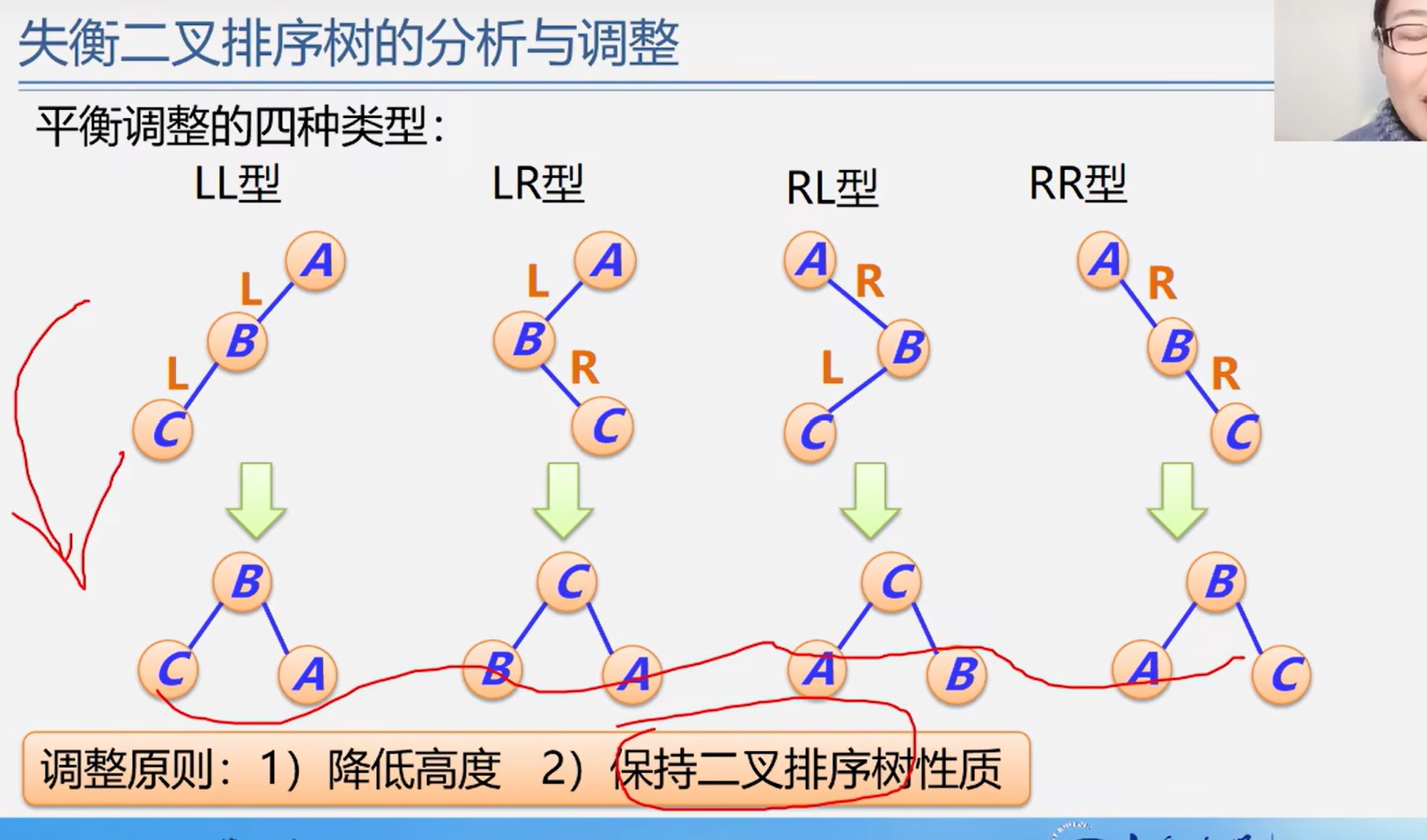
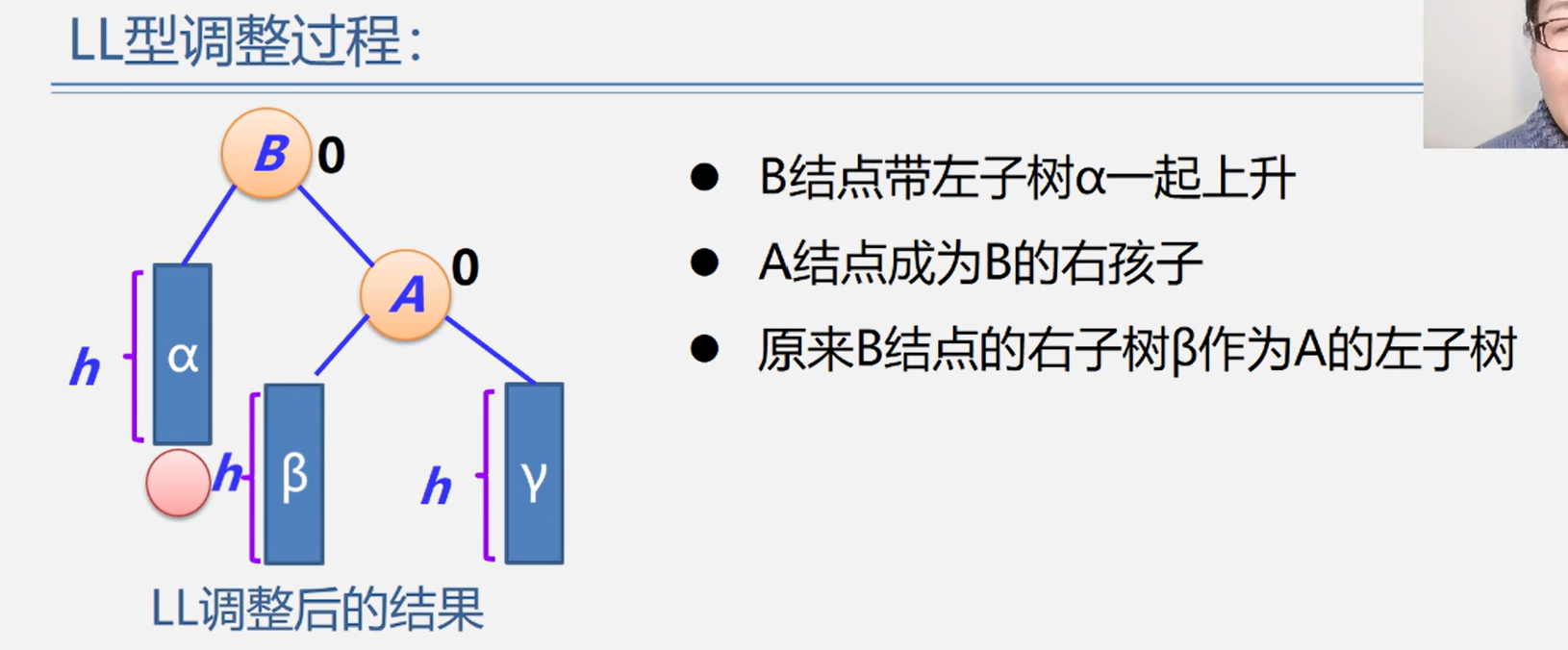
散列表（hash）

1. 定义

   记录储存位置，与关键字的之间的对应关系

2. 散列方法

   

3. 冲突

   不同的关键码通过散列方法映射到同一个位置

4. 同义词

   具有相同地址的关键字

5. 构造散列函数

   

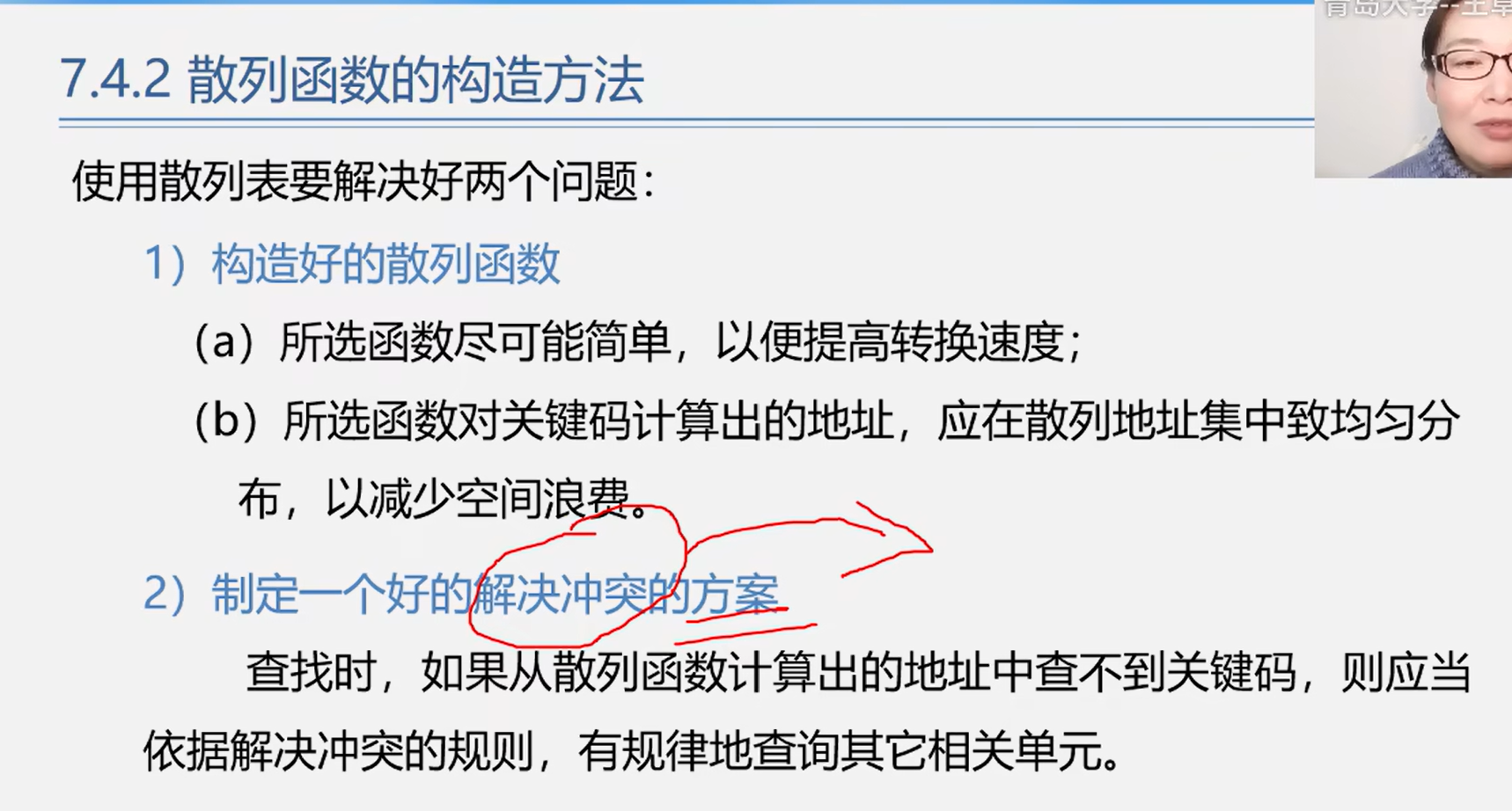
6. 处理冲突

   • 开放地址法

     

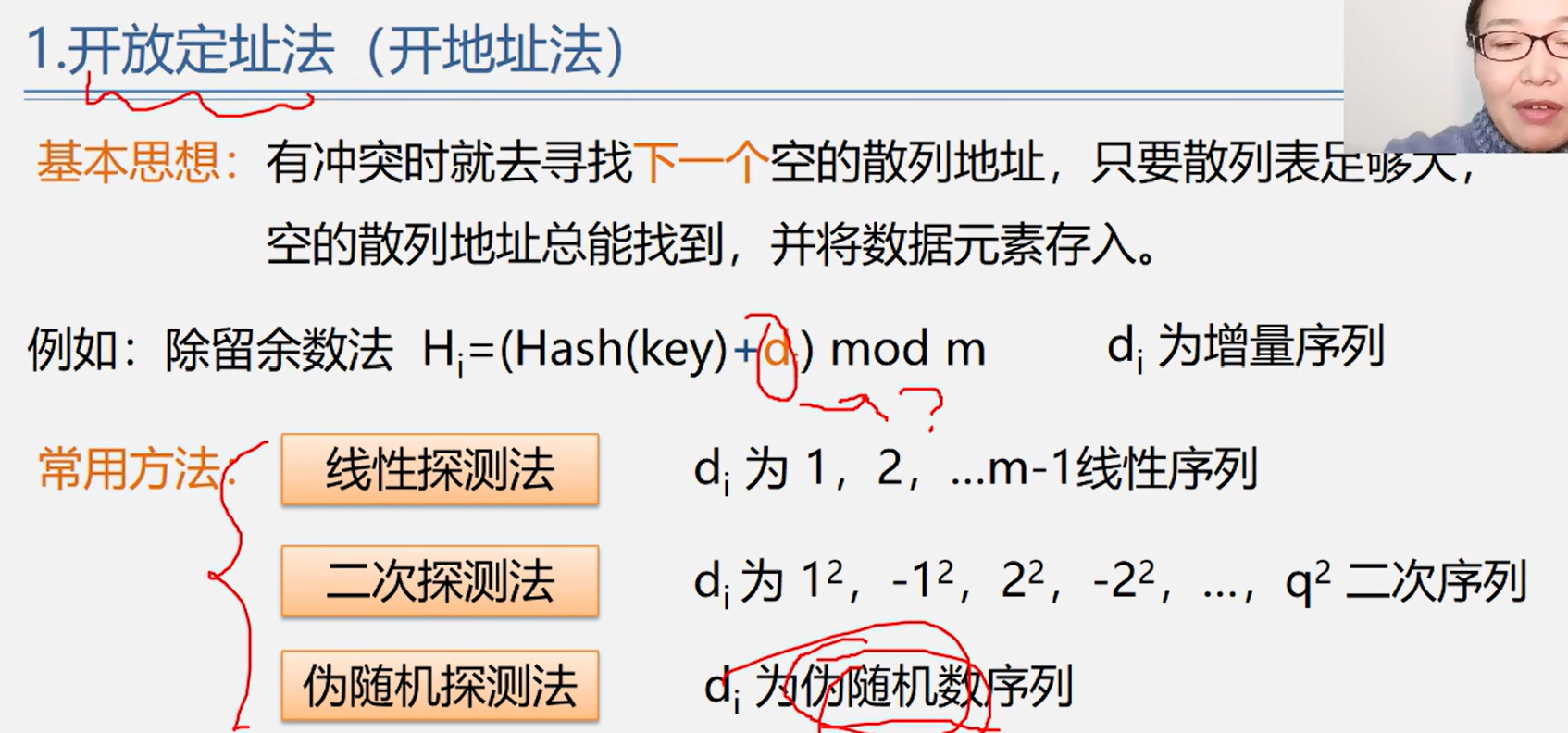
   • 链地址法

     

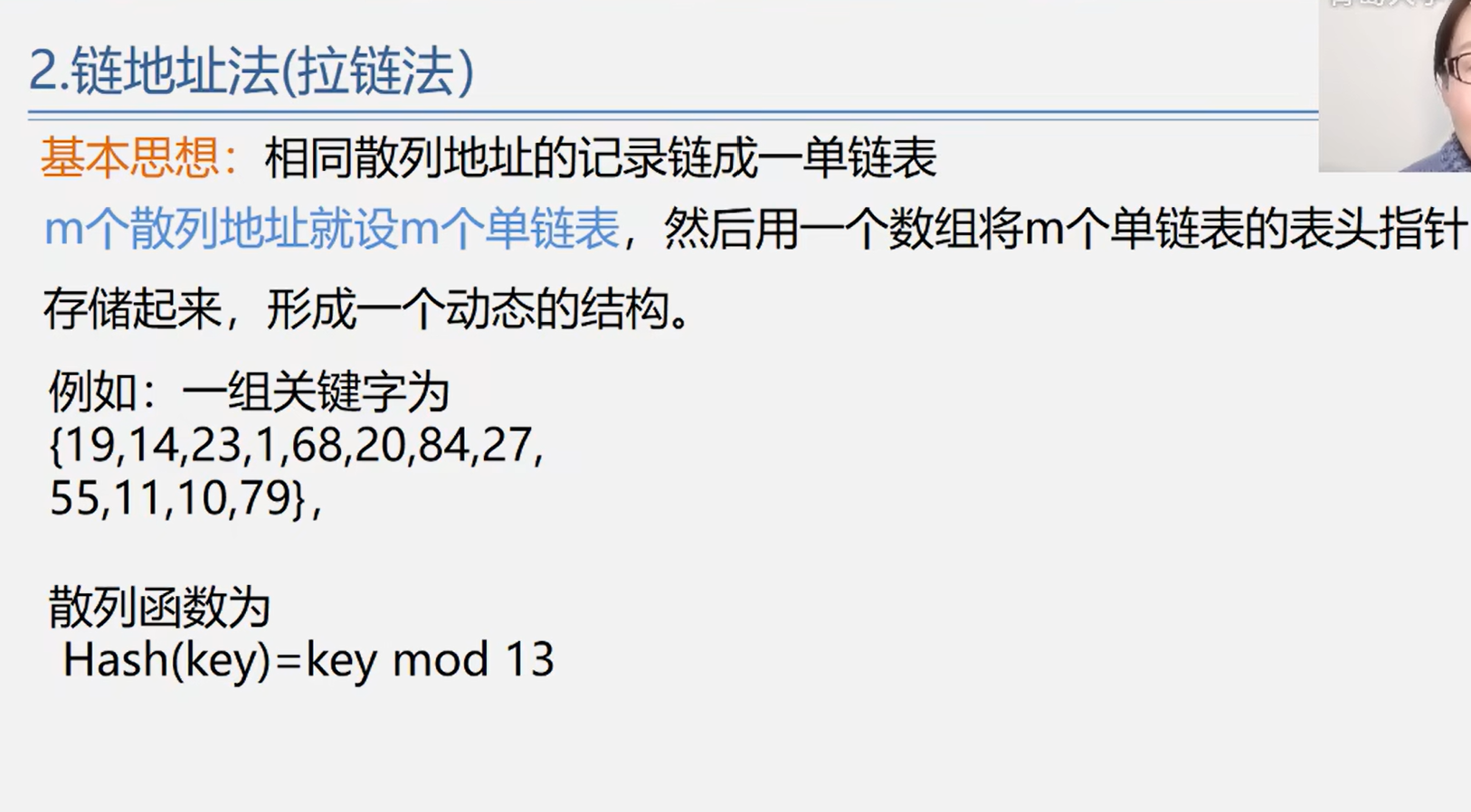
7. 散列表的查找

   

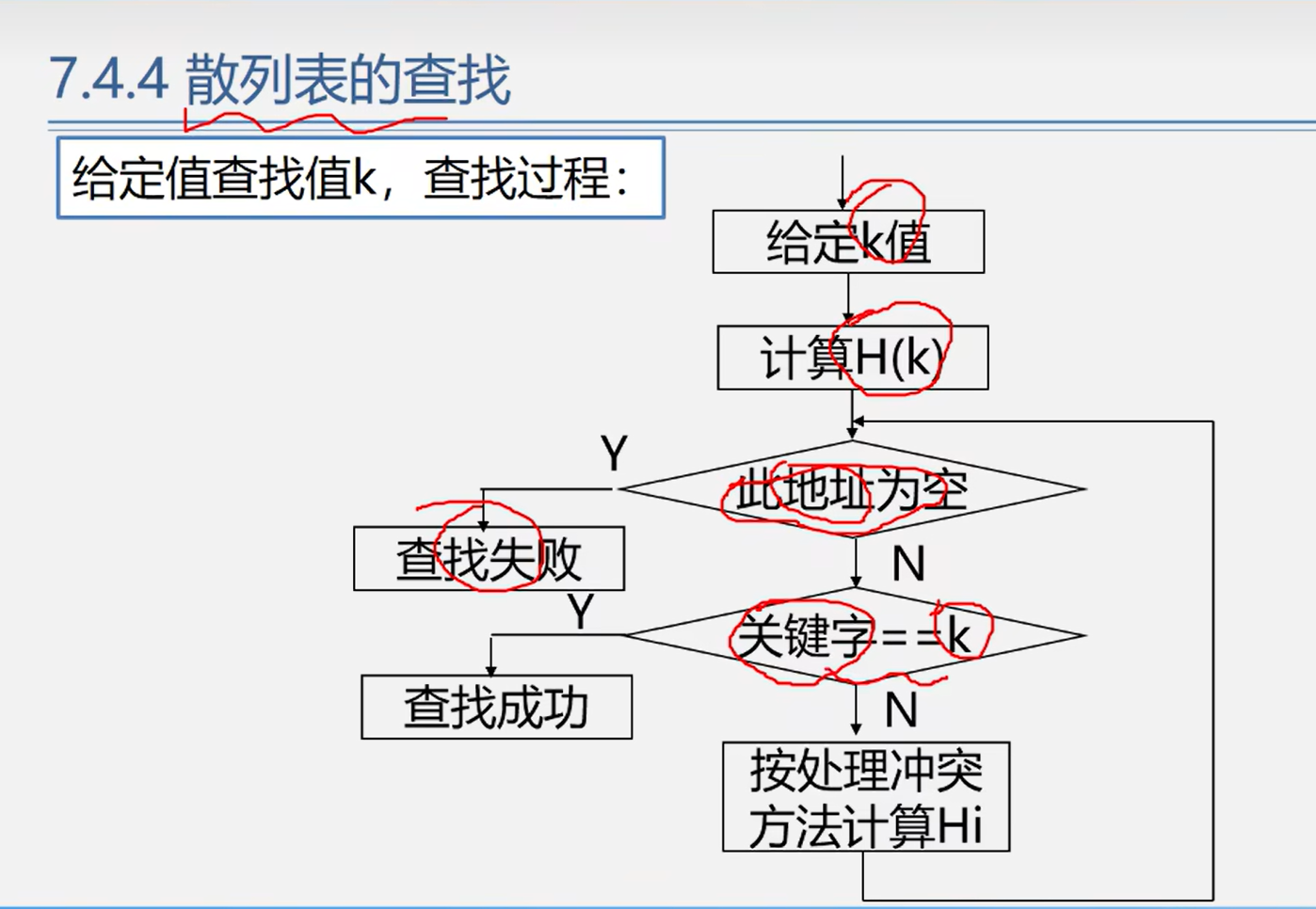
排序

冒泡排序

1. 普通版

   void sort(int ints[],int size){
       for (int i = 0; i < size; ++i) {
           for (int j = 1; j < size-i; ++j) {
               if(ints[j-1]<ints[j]){
                   int tem=ints[j-1];
                   ints[j-1]=ints[j];
                   ints[j]=tem;
               }
           }
       }
   }

2. 根据需要限定范围

选择排序

void sort(int ints[],int size){
    for (int i = 0; i < size; ++i) {
        for (int j = i+1; j < size; ++j) {
            if(ints[i]>ints[j]){
                int tem=ints[i];
                ints[i]=ints[j];
                ints[j]=tem;
            }
        }
    }
}

直接插入排序

1. 对一个有序表插入一个数据

2. 对一个无序的线表排序

      
   void sort(int ints[], int size) {
       for (int i = 1; i < size; ++i) {
           if (ints[i] < ints[i - 1]) {
               int tem=ints[i];
               int j=i-1;
               for (; ints[j] > tem; --j) {
                   ints[j+1]=ints[j];
               }
               ints[j+1]=tem;
           }
       }
   }
      
      

希尔排序

1. 只是对插排分组

      
   void sort(int ints[], int size) {
       int range=size;
       while((range=range/3)>0){
           for (int i = range; i < size; ++i) {
               if (ints[i] < ints[i - range]) {
                   int tem=ints[i];
                   int j=i-range;
                   for (; ints[j] > tem; j-=range) {
                       ints[j+range]=ints[j];
                   }
                   ints[j+range]=tem;
               }
           }
       }
   }
      

堆排序

1. 大根堆

   根节点大于等于左右孩子的value

2. 小根堆

   根节点小于等于左右孩子的value

3. 代码实现

      
   void HeapAdjust(int ints[], int s, int size) {
       int tem = ints[s];
       for (int i = s * 2; i <= size; i *= 2) {
           if (i < size && ints[i] < ints[i + 1]) {
               i++;
           }
           if (tem >= ints[i]) {
               break;
           }
           ints[s] = ints[i];
           s = i;
       }
       ints[s] = tem;
   }
      
   void sort(int ints[], int size) {
       for (int i = size / 2; i > 0; --i) {
           HeapAdjust(ints, i, size);
       }
       for (int i = size; i > 0; --i) {
           int tem = ints[1];
           ints[1] = ints[i];
           ints[i] = tem;
           HeapAdjust(ints, 1, i - 1);
       }
   }
      

归并排序

1. 有序表的合并

   (线性表的合并)[线性表 - chg (tsy244.github.io)]

2. 递归 代码实现

   void merge(int *list1, int list1_size, int *list2, int list2_size) {
       int ints[20] = {-1};
       int list1Sub = 0;
       int list2Sub = 0;
       int intsSub = 0;
       while (list1_size != list1Sub && list2_size != list2Sub) {
           ints[intsSub++] = list1[list1Sub] > list2[list2Sub] ? list1[list1Sub++] : list2[list2Sub++];
       }
       while (list2Sub < list2_size) {
           ints[intsSub++] = list2[list2Sub++];
       }
       while (list1Sub < list1_size) {
           ints[intsSub++] = list1[list1Sub++];
       }
      
       for (int i = 0; i < list1_size+list2_size; ++i) {
           list1[i]=ints[i];
       }
   }
      
      
   void sort(int ints[], int size) {
       if (size > 1) {
           int *list1 = ints;
           int list1_size = size / 2;
           int *list2 = ints + list1_size;
           int list2_size = size - list1_size;
      
           sort(list1, list1_size);
           sort(list2, list2_size);
           merge(list1, list1_size, list2, list2_size);
      
       }
   }

3. 迭代代码实现

快速排序

1. 普通实现的快速排序

int findMidSub(int ints[],int low,int high){
    ints[0]=ints[low];
    while(low<high){
        while(low<high&&ints[high]>ints[0]){
            high--;
        }
        ints[low]=ints[high];
        while(low<high&&ints[low]<ints[0]){
            low++;
        }
        ints[high]=ints[low];
    }
    ints[low]=ints[0];
    return low;
}
   
   
void sort(int ints[], int low,int high) {
    if(low<high){
        int midSub=findMidSub(ints,low,high);
   
        sort(ints,low,midSub-1);
        sort(ints,midSub+1,high);
    }
}
   

2. 改良的快排

   int findMidSub(int ints[],int low,int high){
       int mid=low+(high-low)/2;
       if(ints[mid]>ints[high]){
           int tem=ints[mid];
           ints[mid]=ints[high];
           ints[high]=tem;
       }
       if(ints[low]>ints[high]){
           int tem=ints[low];
           ints[low]=ints[high];
           ints[high]=tem;
       }
      
       if(ints[low]<ints[mid]){
           int tem=ints[mid];
           ints[mid]=ints[low];
           ints[low]=tem;
       }
       ints[0]=ints[low];
      
      
       while(low<high){
           while(low<high&&ints[high]>ints[0]){
               high--;
           }
           ints[low]=ints[high];
           while(low<high&&ints[low]<ints[0]){
               low++;
           }
           ints[high]=ints[low];
       }
       ints[low]=ints[0];
       return low;
   }
      
      
   void sort(int ints[], int low,int high) {
       if(low<high){
           int midSub=findMidSub(ints,low,high);
      
           sort(ints,low,midSub-1);
           sort(ints,midSub+1,high);
       }
   }
      

基数排序（桶排序/箱排序）

1. 根据不同的关键词经行排序，所以桶排序适合于关键词的个数