树和二叉树

[TOC]

树和二叉树

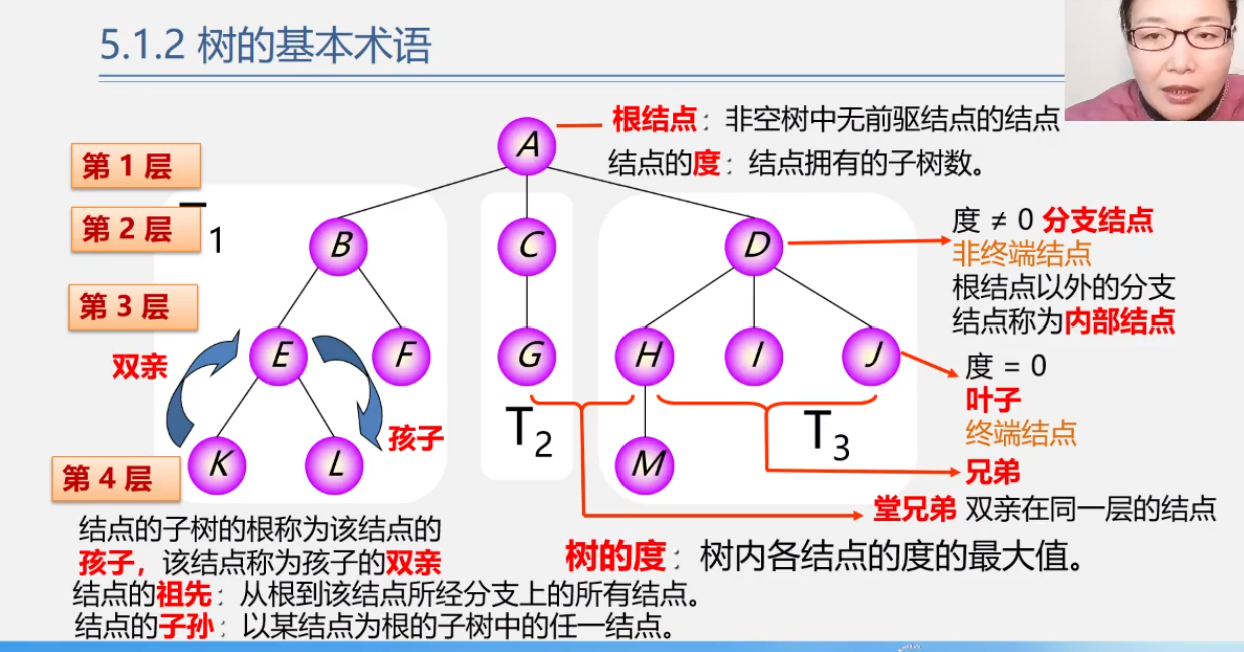
树的基本

  1. 一个根和若干的子树

  2. 基本术语

  3. 树的类别

    • 有序树

      子树有位置要求

    • 无序树

      子树无要求

      意思是：1，2，3，这三颗子树，无论如何排列都是一个树

  4. 森林

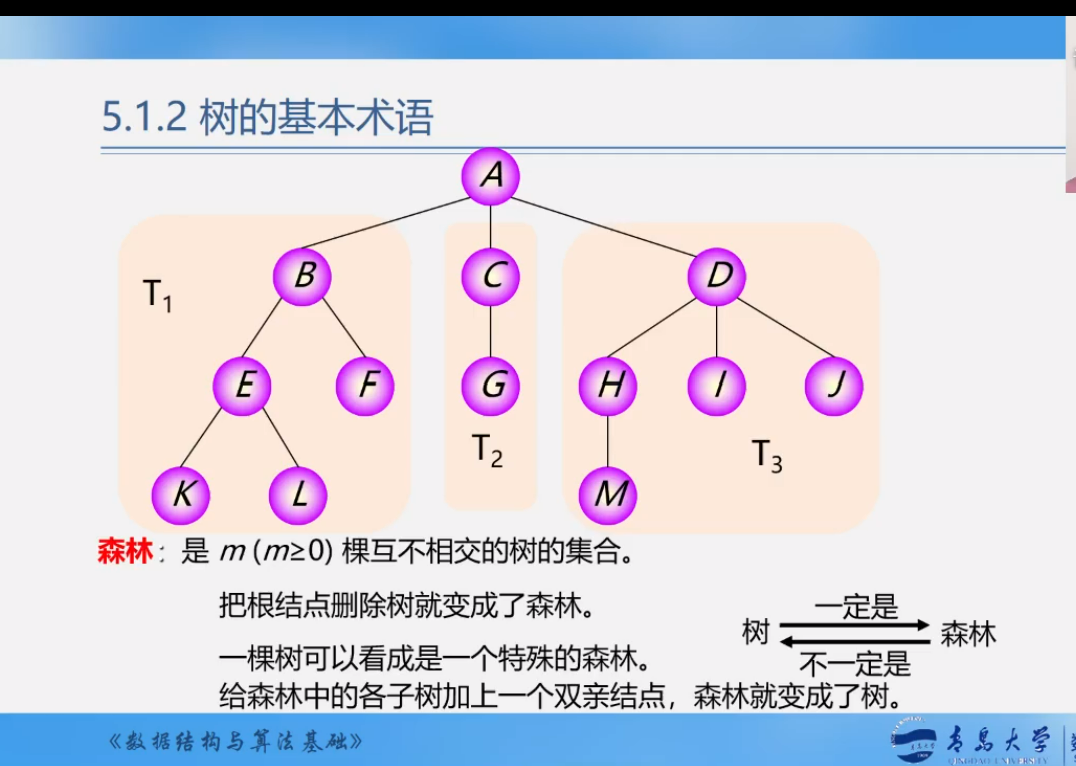
  5. 树和线性结构的比较

    • 树是一对多
    • 线性结构是一对一

二叉树

  1. 每个节点最多有两个度

  2. 二叉树是个有序树（但是不是树的特殊情况）

  3. 二叉树可以是一 个空集

  4. 二叉树必须要分左子树还是右子树，即使只有一颗子树也要分（但是树可以不分，所以这就是二叉树不是树的原因）

  5. 二叉树的基本形态

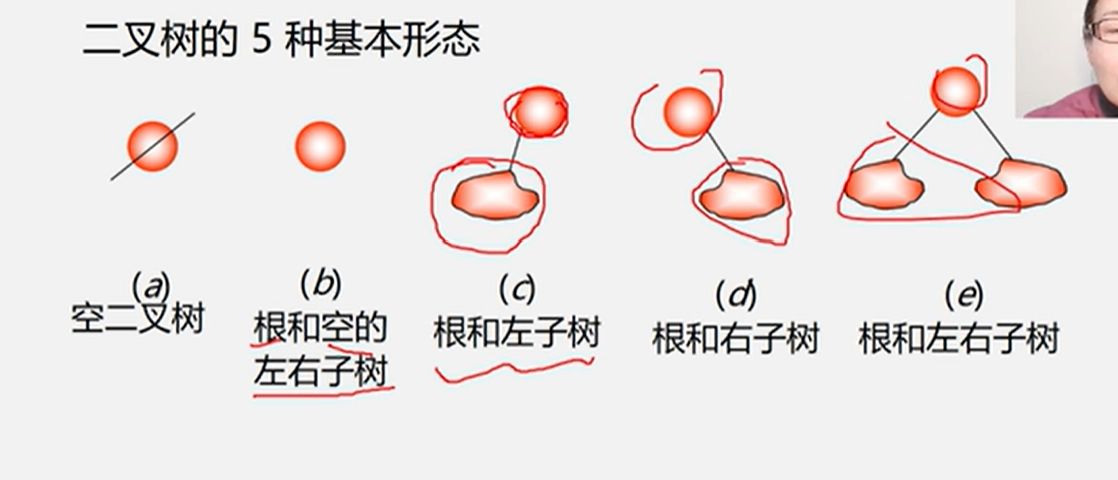
  6. 二叉树的抽象类型定义

  7. 二叉树的性质

    • 在二叉树的第i层最多有2^i-1^ 个节点，最少有一个

    • 深度为k的二叉树最多有2^k^ -1个节点

    • 对任何一颗二叉树T如果叶子树为n0=n2+1

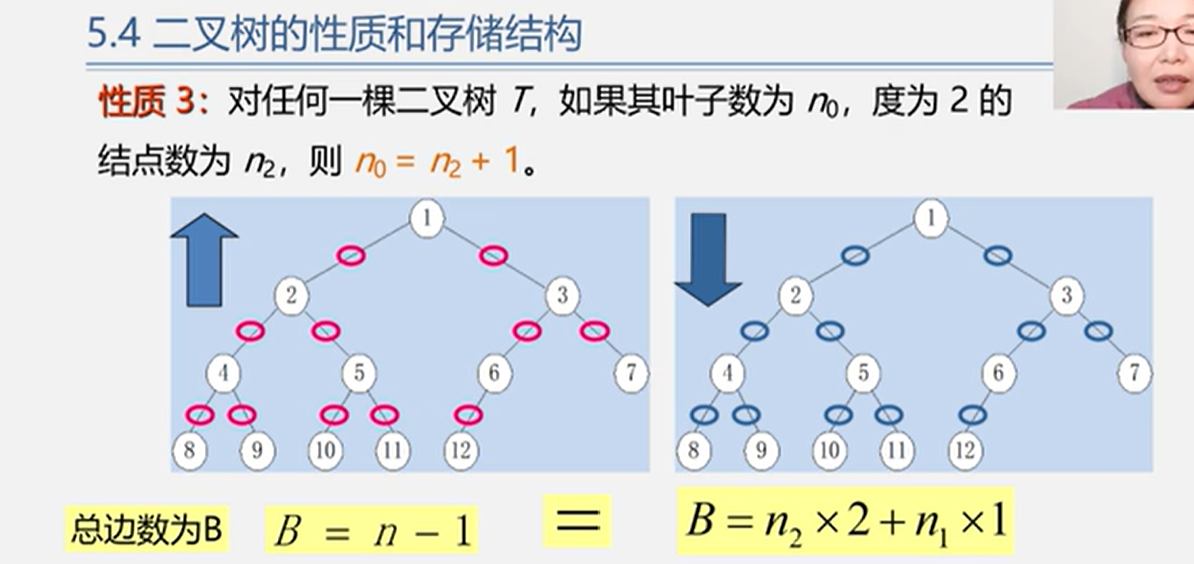
    • B=n-1

      从下网上看，因为除了根节点每个节点都会产生一条边，所以n-1（除了根节点）个节点会产生n-1个边

    • n2 *2 +n1*1

      从上往下看，因为，每一个度为2的节点都会产生两条边，每一度为1的节点会产生一个边

    • 满二叉树

      • 每一层都达到最大的节点数
      • 叶子节点出现在最后一层

    • 完成二叉树

      • 二叉树中有编号的与满二叉树的标号对应

      • 在满二叉树中去除立连续的节点，剩下的也是完全二叉树

      • 满二叉树一定是完全二叉树

      • 完全二叉树的性质

        性质三

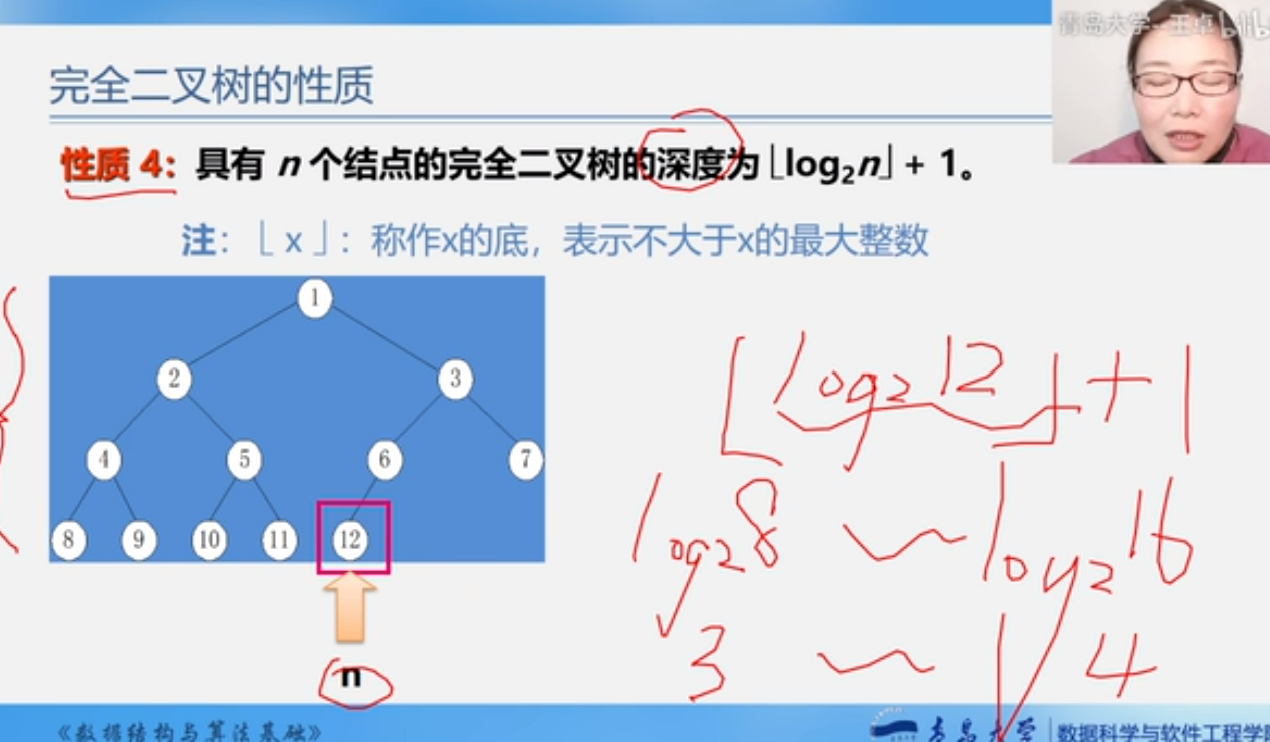
        性质四

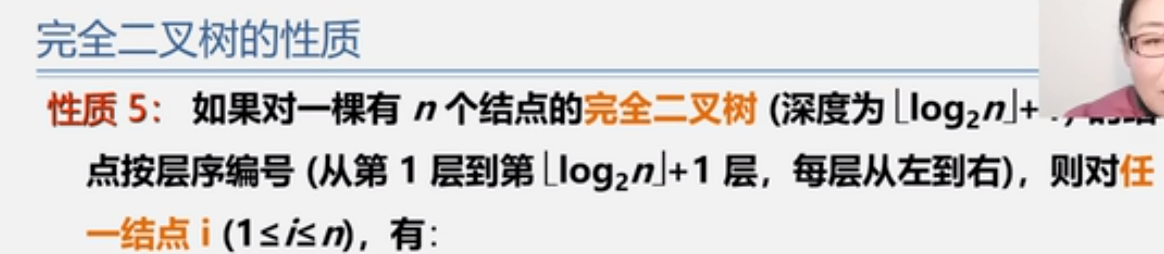
  8. 二叉树的存储结构

    • 顺序结构
    • 链式结构
      • 二叉链表
      • 三叉链表

  9. 二叉树的链式存储的储存结构

    二叉链表

    1
    2
    3
    4
    typedef struct BiNode{
        TElemType data;
        struct BiNode *lChild,*rChild;
    }BiNode,*BiTree;

    三叉链表(多了一个指向双亲的指针)

    1
    2
    3
    4
    5
    typedef struct BiNode{
        TElemType data;
        struct BiNode *lChild,*parent,*rChild;
    }BiNode,*BiTree;

    • 在n个节点的二叉链表中，必有2n个链域，除了根节点没有双亲，所以一定会有n-1个节点的链域存放指针，指向非空的子女节点。

    所以一共有n+1个空指针域

  10. 二叉树的遍历

  • 先序遍历

    先访问根节点，再访问左子树，再访问右子树

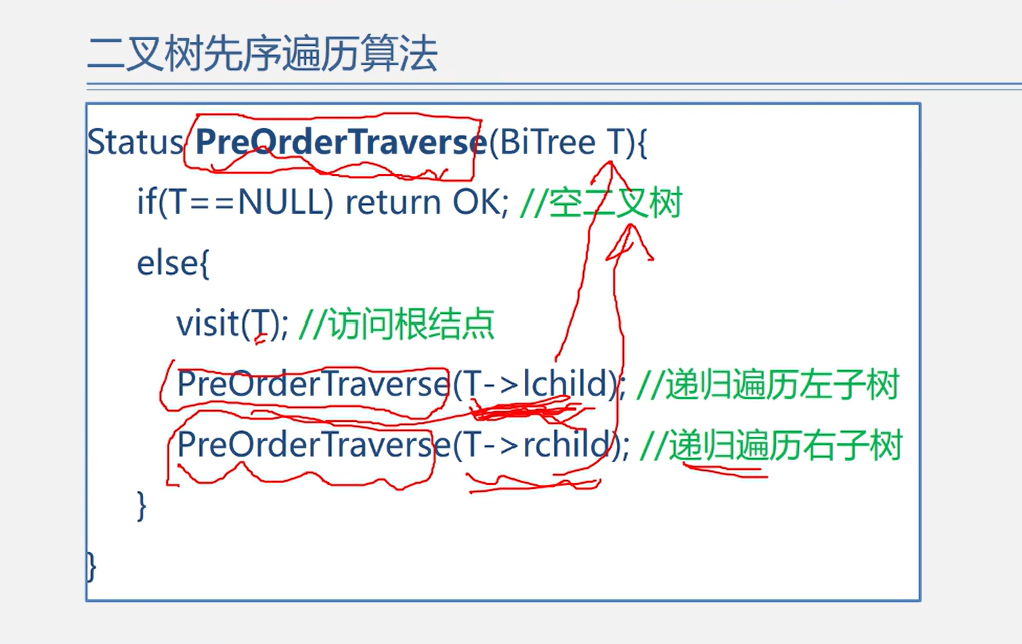
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    void visit(BiTree T){
        printf("%c",T->data);
    }

    status PreOrderTraverse(BiTree T){
        if(T==NULL){
            return false;
        }else {
            visit(T);
            PreOrderTraverse(T->lChild);
            PreOrderTraverse(T->rChild);
        }
    }

  • 中序遍历

    先访问左子树，再访问根节点，再访问右子树

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    void visit(BiTree T){
        printf("%c",T->data);
    }

    status PreOrderTraverse(BiTree T){
        if(T==NULL){
            return false;
        }else {
            PreOrderTraverse(T->lChild);
            visit(T);
            PreOrderTraverse(T->rChild);
        }
    }

  • 后续遍历

    先访问左子树，在访问右子树，最后访问根节点 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14

    void visit(BiTree T){
        printf("%c",T->data);
    }

    status PreOrderTraverse(BiTree T){
        if(T==NULL){
            return false;
        }else {
            PreOrderTraverse(T->lChild);
            PreOrderTraverse(T->rChild);
            visit(T);
        }
    }

  • 例题：

    使用二叉树表达算术表达式

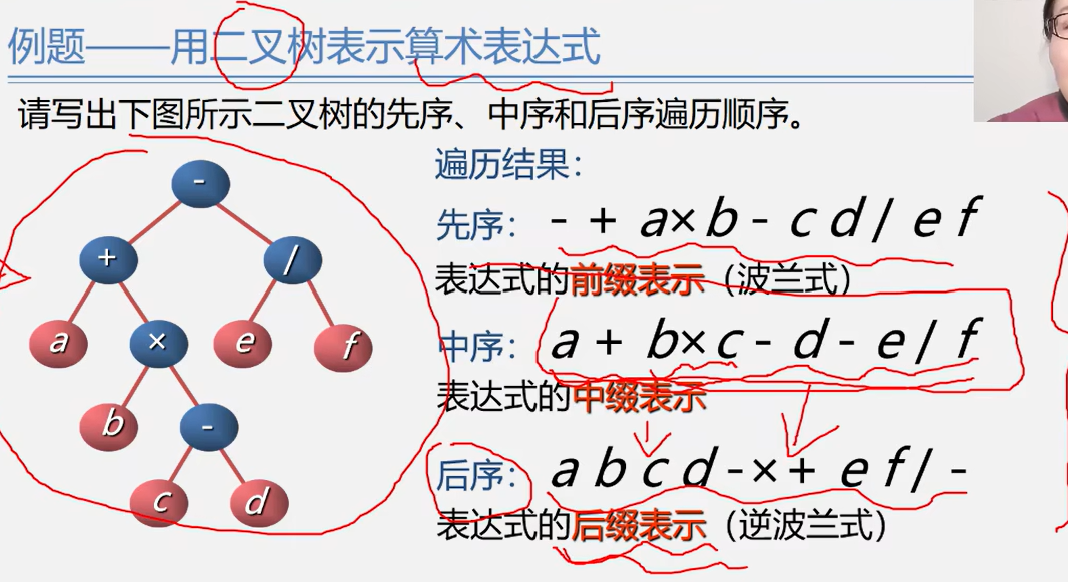
  • 递归遍历的算法分析

    img

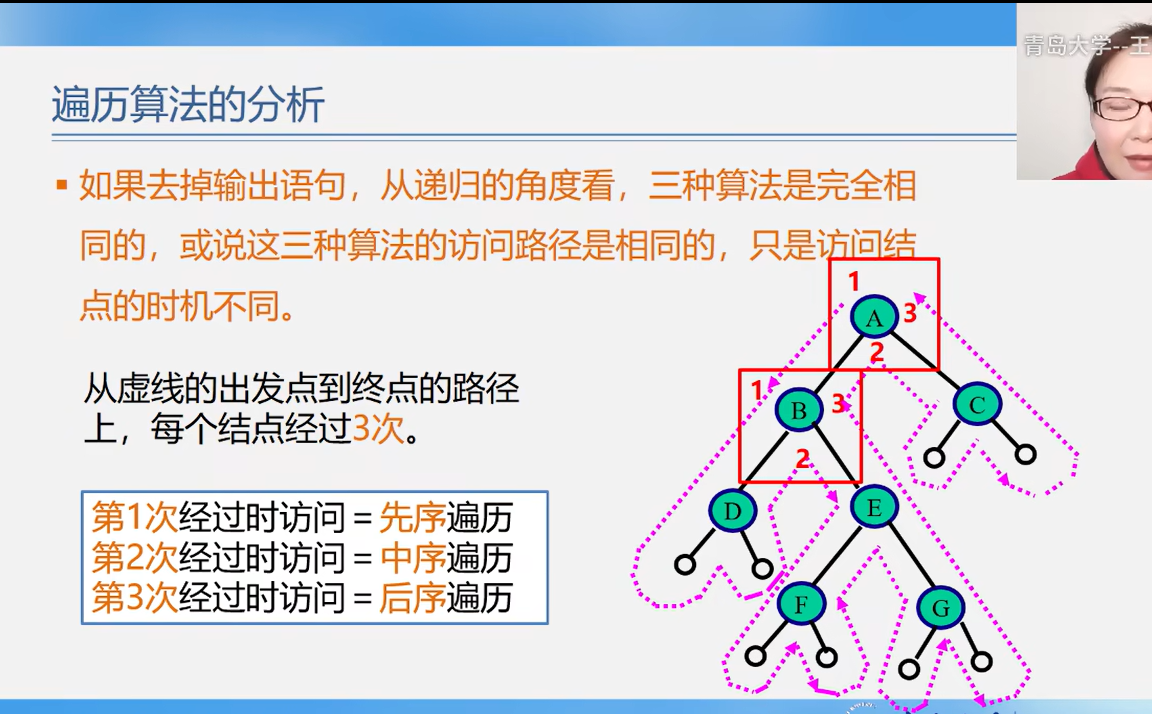
    从虚线出发到每一个终点路径每个节点经历3次

  • 非递归遍历

    中序遍历

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29

    #include "iostream"
    #include "stack"

    #define status int
    #define OK 1
    #define ERROR (-1)
    #define true 1
    #define false 0
    #define TElemType char
    #define SIZE 100
    status InOrderTraverse(BiTree& T){
        std::stack<BiTree> stack;//申请一个栈
        BiTree moveNode=T;
        while(!stack.empty()||moveNode!= nullptr){
            if(moveNode!= nullptr){
                stack.push(moveNode);
                moveNode=moveNode->lChild;
            }else{
                auto p=stack.top();//得到栈首的元素
                std::cout<<p->data<<" ";
                stack.pop();
                moveNode=p->rChild;
            }
        }
        return OK;
    }


  • 层次遍历

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    status LeveIOrder(BiTree& biTree){
        std::queue<BiTree> queue;
        BiNode* pMove=biTree;
        queue.push(biTree);
        while(!queue.empty()){
            if(queue.front()->lChild!= nullptr){
                queue.push(queue.front()->lChild);
            }
            if(queue.front()->rChild!= nullptr){
                queue.push(queue.front()->rChild);
            }
            std::cout<<queue.front()->data<<" ";
            queue.pop();
        }
    }

  1. 二叉树的创建

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    status CreatBitree(BiTree* biTree){
        TElemType ch;
        scanf("%c",&ch);
        if(ch=='#'){
            return OK;
        }else {
            (*biTree)=(BiNode*) malloc(sizeof(BiNode));
            (*biTree)->lChild=NULL;
            (*biTree)->rChild=NULL;
            (*biTree)->data=ch;
            CreatBitree(&(*biTree)->lChild);
            CreatBitree(&(*biTree)->rChild);
        }
    }

    • 定义：

      ‘#’代表没有节点

    所以上面代码的实现是，根据符号来确定是否要创建一个二叉树

  2. 二叉树的复制

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    status Copy(BiTree T, BiTree *newBitree) {
        if (T != NULL) {
            *newBitree = (BiTree) malloc(sizeof(BiNode));
            (*newBitree)->lChild=NULL;
            (*newBitree)->rChild=NULL;
            (*newBitree)->data=T->data;
            Copy(T->lChild,&(*newBitree)->lChild);
            Copy(T->rChild,&(*newBitree)->rChild);
        }
        return OK;
    }

  3. 计算二叉树的深度

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    int Depen(BiTree biTree){
        if(biTree==NULL){
            return 0;
        }else{
            m= Depen(biTree->lChild);
            n= Depen(biTree->rChild);
        }
        if(n>m){
            return (n+1);
        }else{
            return m+1;
        }
    }

  4. 计算二叉树的节点数

    1
    2
    3
    4
    5
    6
    7
    8
    int NodeCount(BiTree biTree) {
        if (biTree != NULL) {
            return NodeCount(biTree->lChild)+ NodeCount(biTree->rChild)+1;
        }else {
            return 0;
        }

    }

  5. 计算叶子节点的个数（叶子节点是左右孩子都为NULL的节点）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    status DestroyBiTree(BiTree *biTree) {
        if (*biTree == NULL) {
            return 0;
        }
        if ((*biTree)->lChild != NULL) {
            DestroyBiTree(&(*biTree)->lChild);
        }
        if ((*biTree)->rChild != NULL) {
            DestroyBiTree(&(*biTree)->rChild);
        }
        printf("  %c", (*biTree)->data);
        free((*biTree));
        (*biTree)==NULL;
        return 0;
    }

  6. 线索二叉树

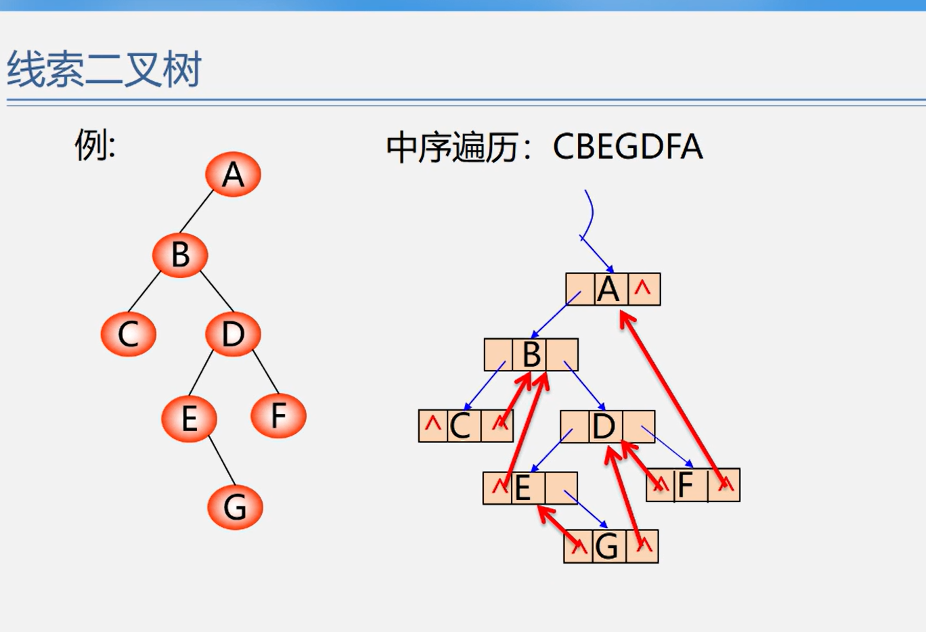
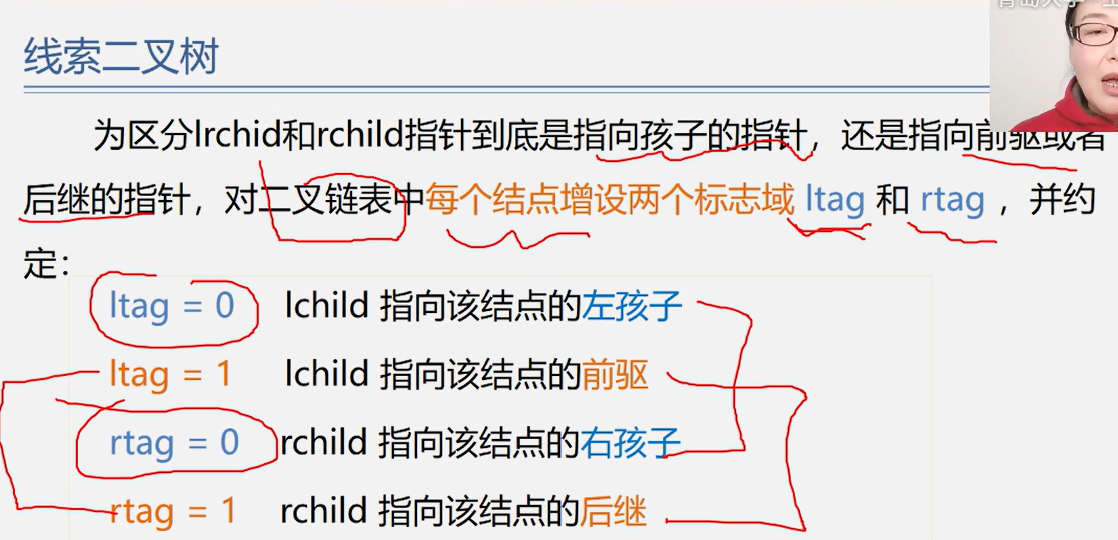
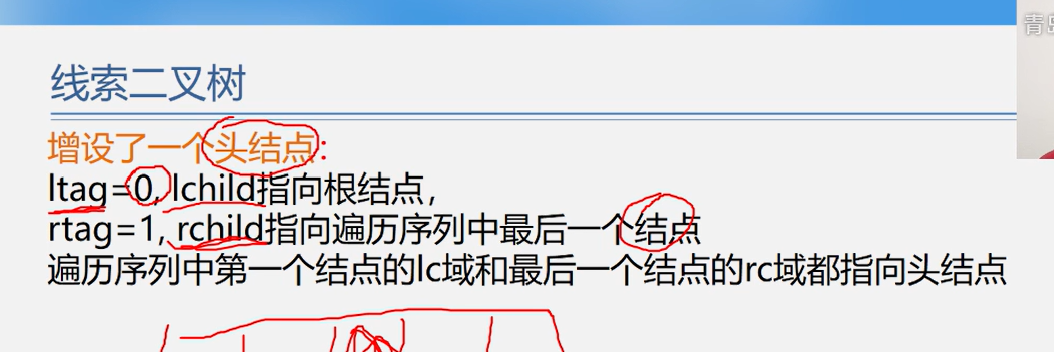
树和森林

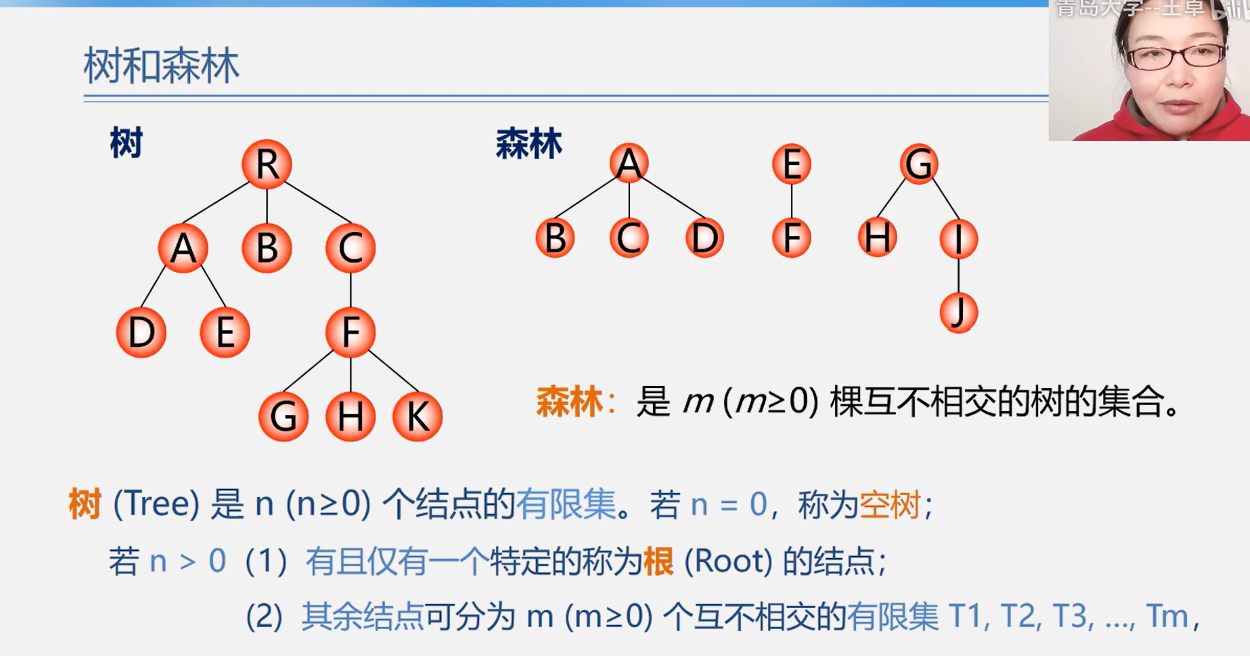
树的存储结构

双亲表示法

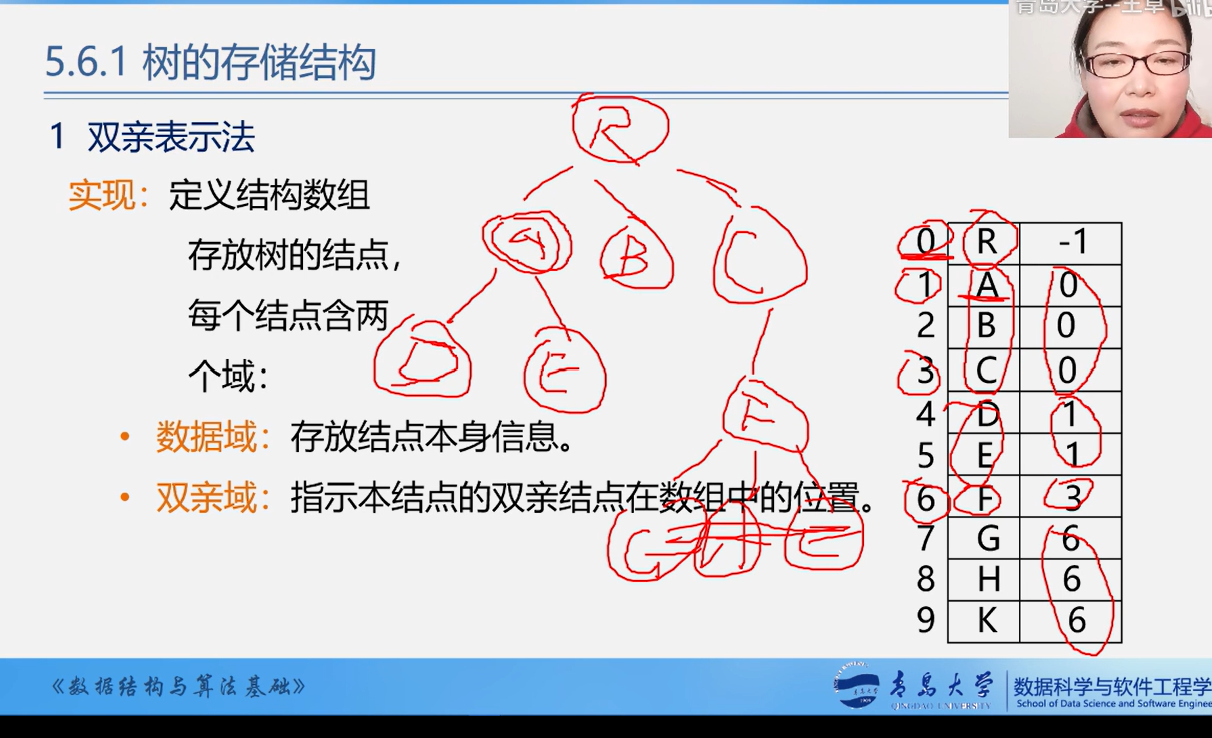
其中A是虚拟的头节点

代码：

1
2
3
4
5
6
7
8
9
typedef struct PTNode{
    TElemType data;
    int parent;
}PTNode;

typedef struct{
    PTNode nodes[BUFSIZ];
    int r,n;//存放根节点和节点个数
}PTree;

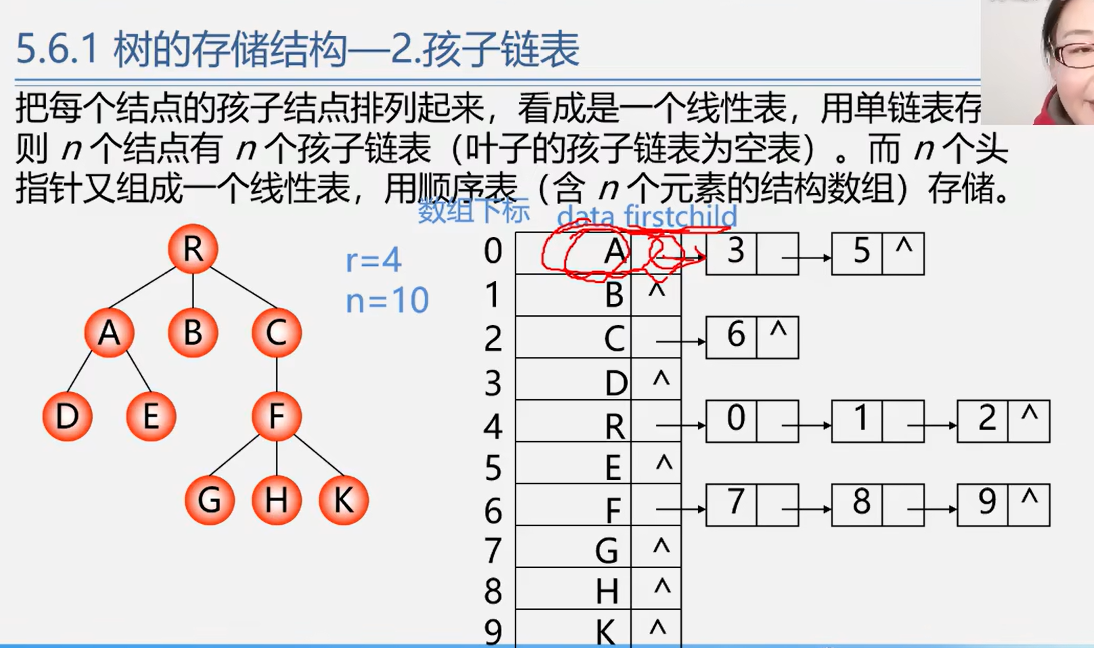
孩子链表

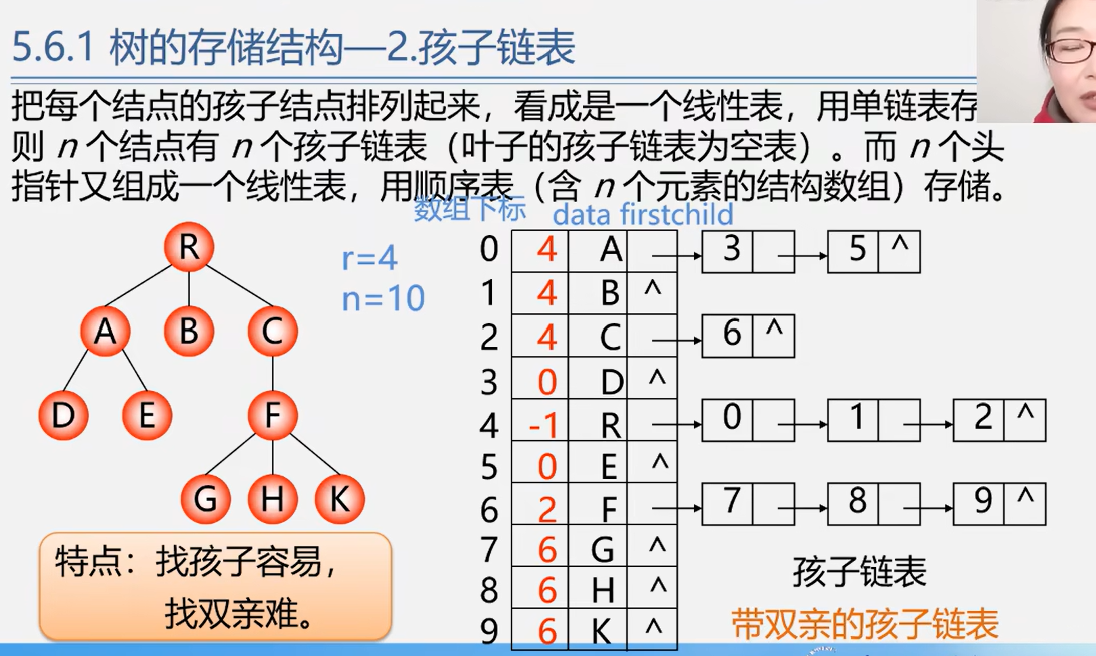
带双亲的孩子链表

只是在孩子链表的基础上多加了双亲的位置

孩子兄弟表示法（二叉树表示法，二叉链表表示法）

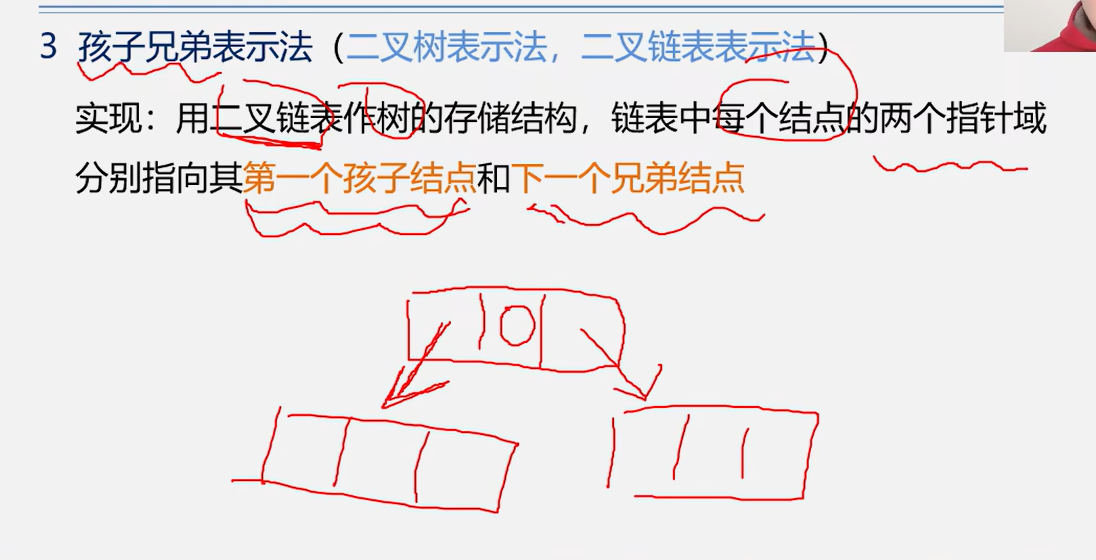
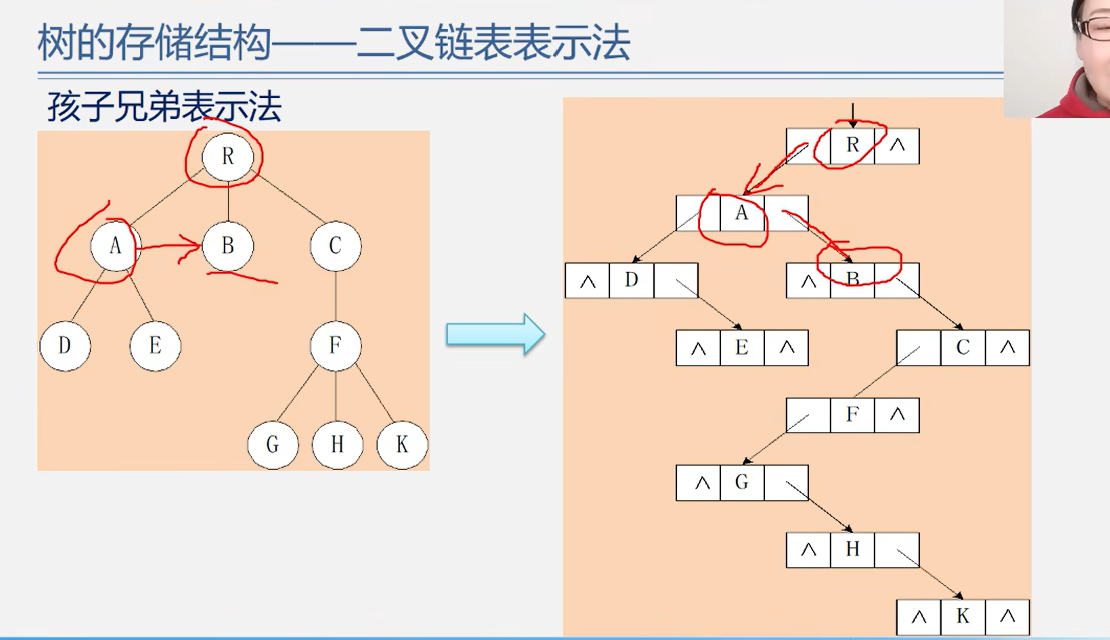
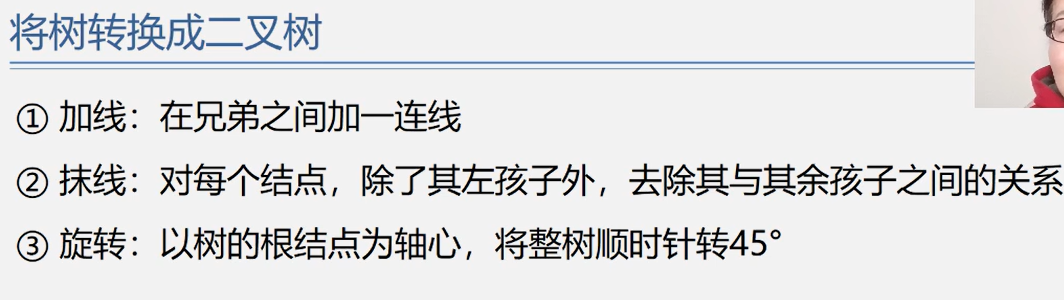
  • 将树转换为二叉树

    兄弟相连留长子

    意思是：将兄弟的连起来，只保留双亲与长子的连线

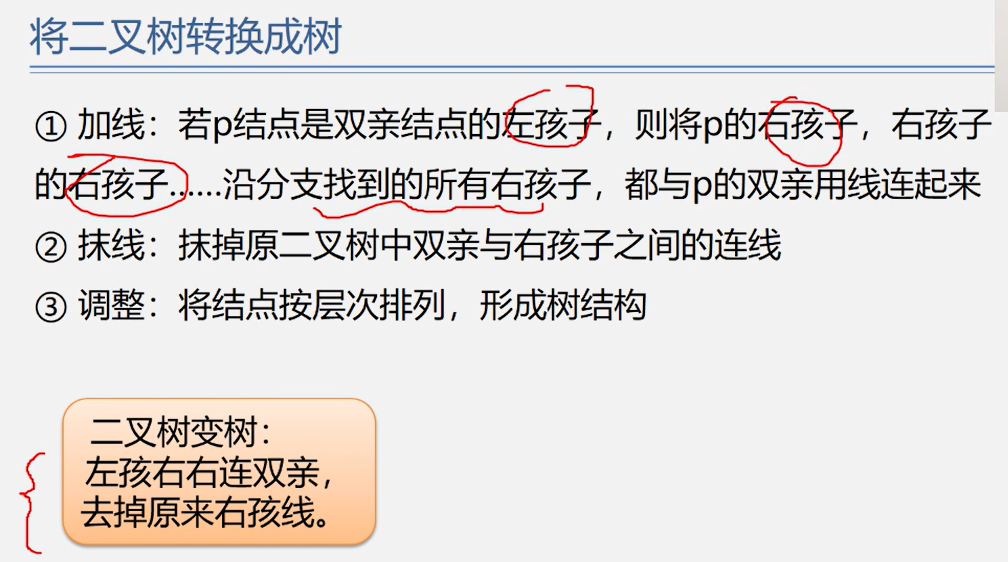
  • 将兄弟二叉树，转变为普通的树

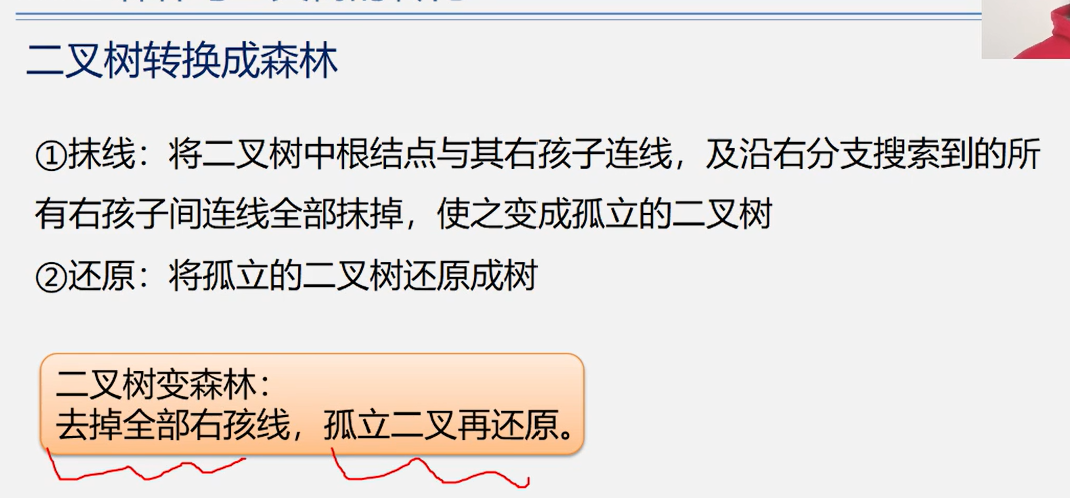
    左孩子右右连双亲，去掉原来的右孩子线

森林和二叉树的转化

  1. 树变二叉树根相连

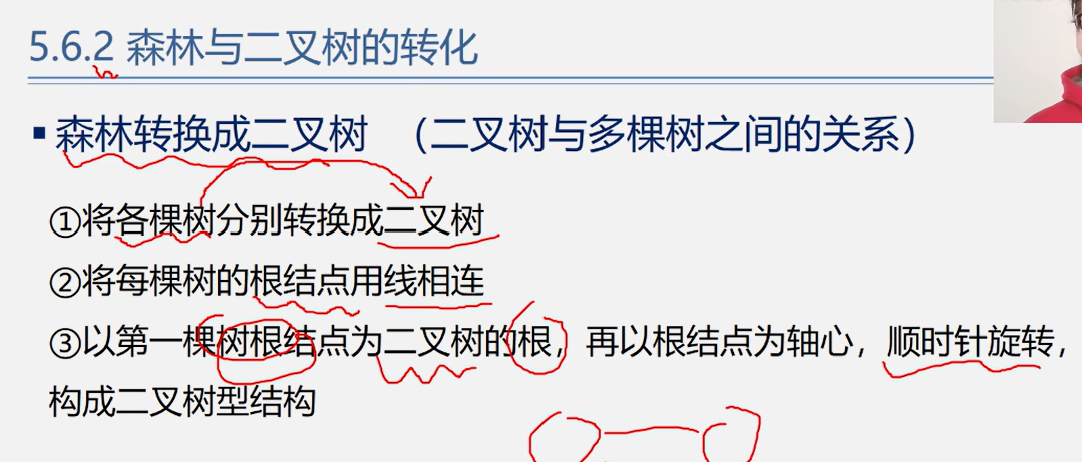
  2. 二叉树变森林

树的遍历

  1. 先根

    如树不为空，那么先遍历根然后在遍历各个子树

  2. 后根

    若树不为空，后根遍历各课子树，然后访问根节点

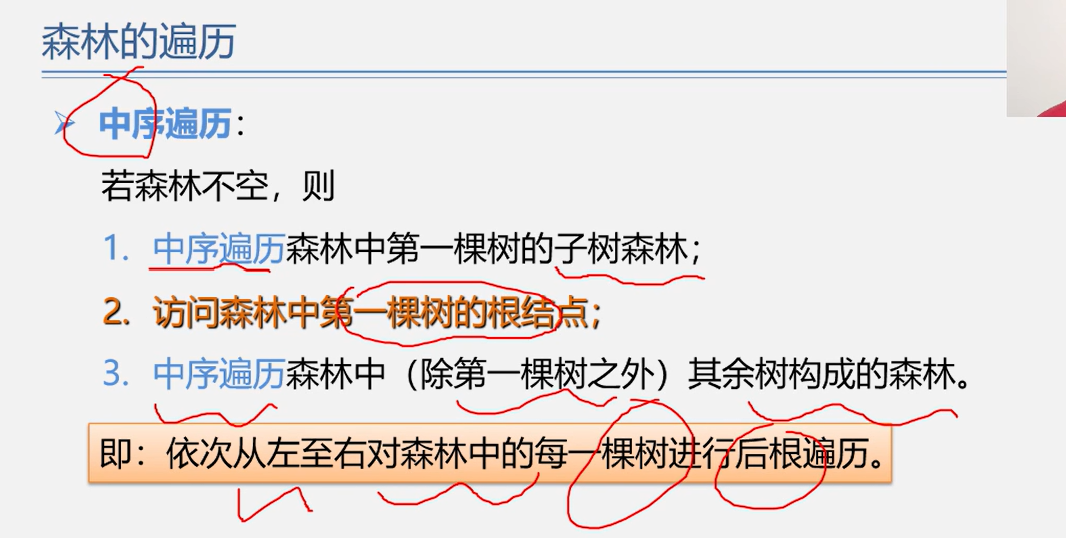
森林的遍历

和二叉树的遍历方式一致

  1. 先序遍历

  2. 中序遍历

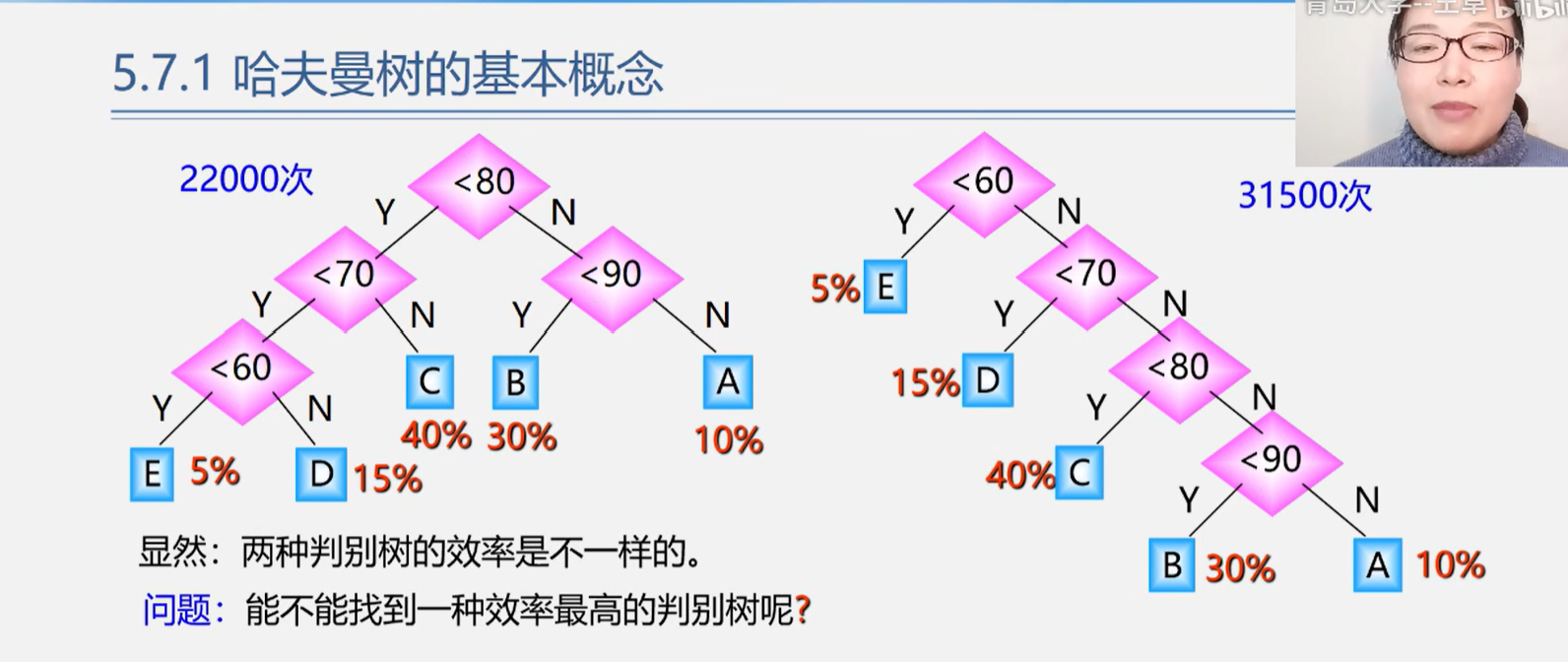
哈夫曼树（最优二叉树）

判断树

左边是改进的选择判断语句

右边是普通的选择判断语句

  1. 基本概念

    • 路径

      从一个结点到另一个结点的分支构成了结点间的路径

    • 结点的路径长度

      两结点间的路径上的分支数

      A->D 的路径长度是 2

    • 树的路径长度

      从根结点到每个结点的路径长度之和

    • 权

      将树中的结点赋一个有某种含义的数值，称为结点的权

    • 结点的带权路径长度

      从根到该节点之间的路径长度×该节点权的结果

    • 树的带权路径长度

      树中所有的叶子结点的带权路径长度之和

哈夫曼树

最优树，也就是带权路径长度最短的树

  1. 满二叉树不一定是最优二叉树

哈夫曼树的特点

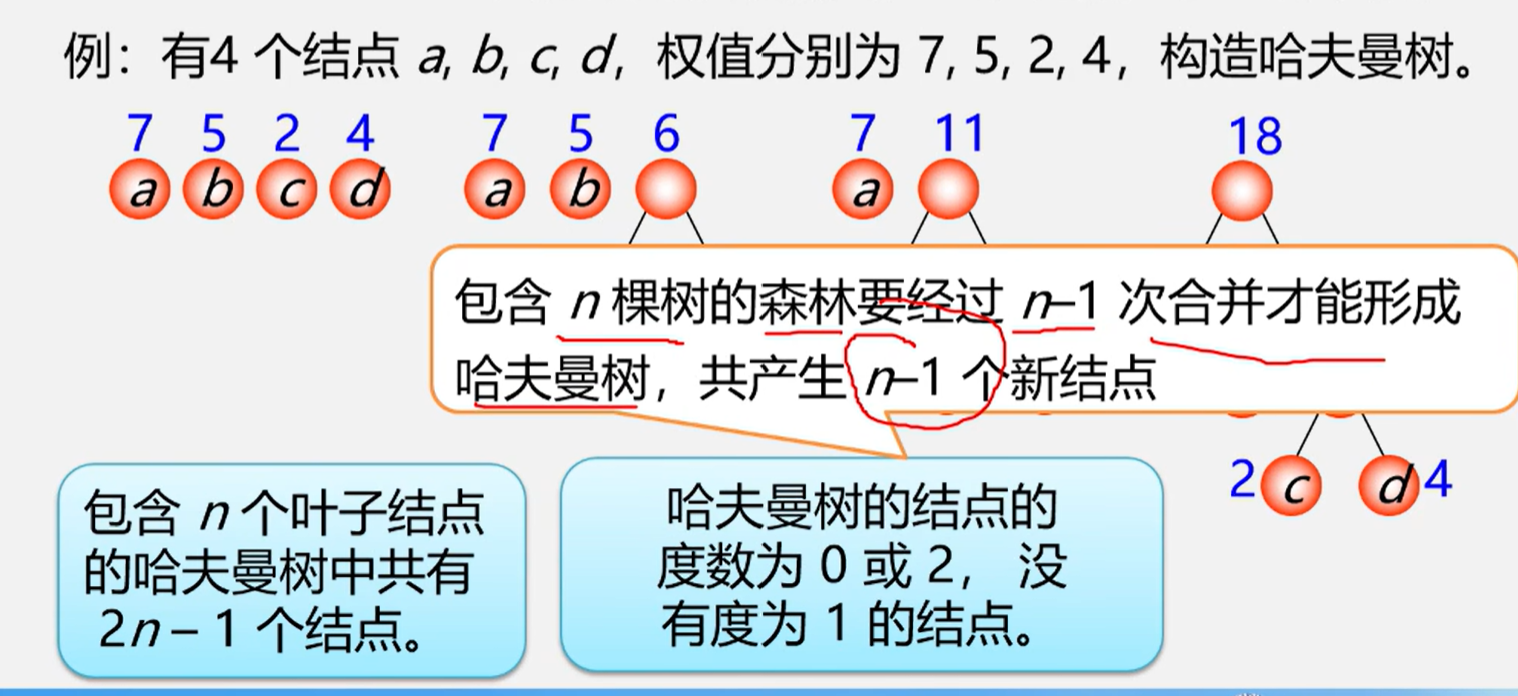
  • 只有度（子树个数 ）0为0或2的结点
  • 一共有2n-1个结点，且新构成的结点都是度为二的结点，原来的结点都是度为一的结点
  • 一共有n个叶子结点（原来的结点，也就是度为0的结点）

哈夫曼树的构造

  1. 权值越大的先构造（贪心算法）

步骤

  • 构造森林全是根
  • 选用两小造新树
  • 删除两小添新人
  • 重复2，3剩单根

删除两小的意思是：删除原来队列里面的两个小的

直到剩下一棵树，就是哈夫曼树

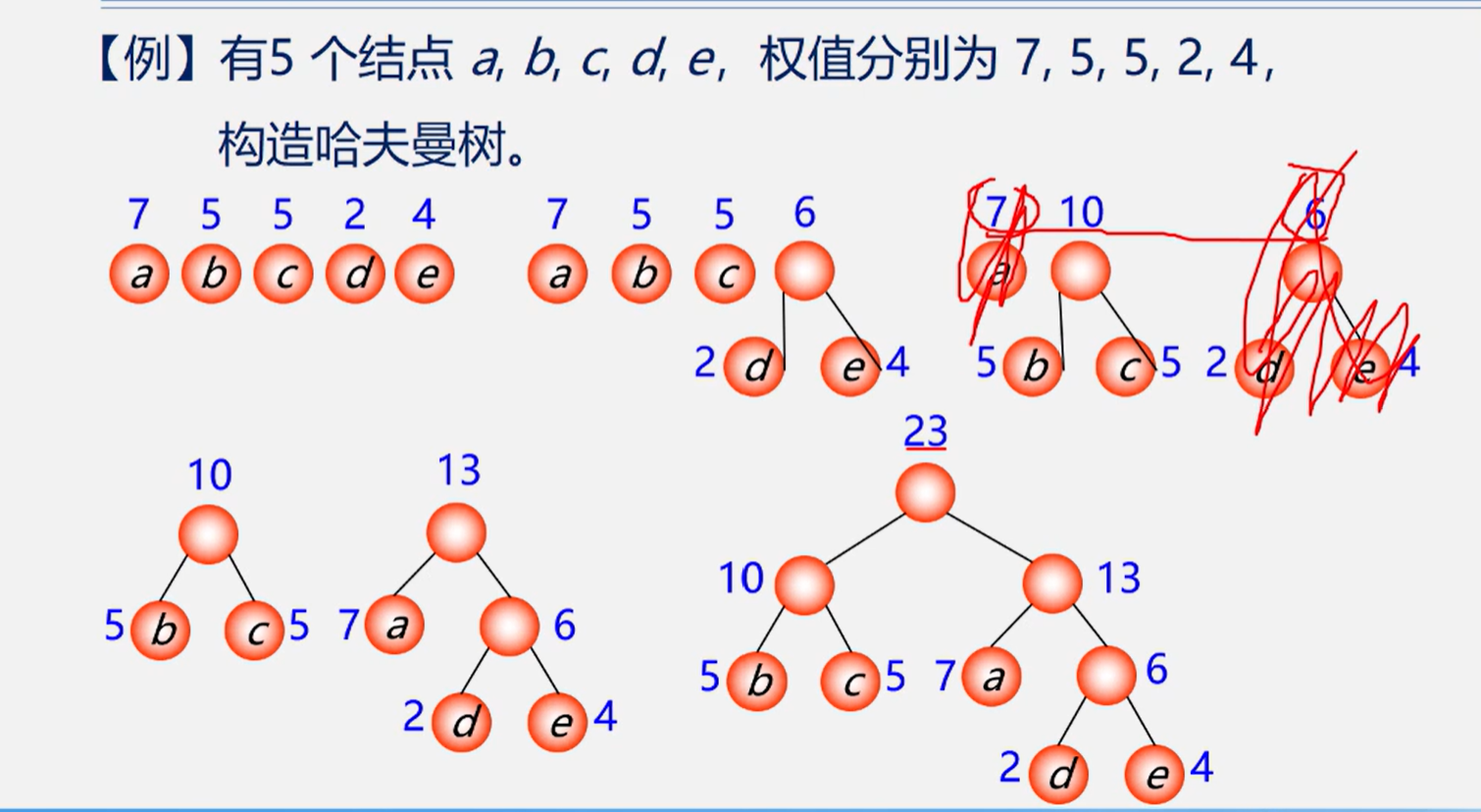
下面是一个例题

  1. 代码实现

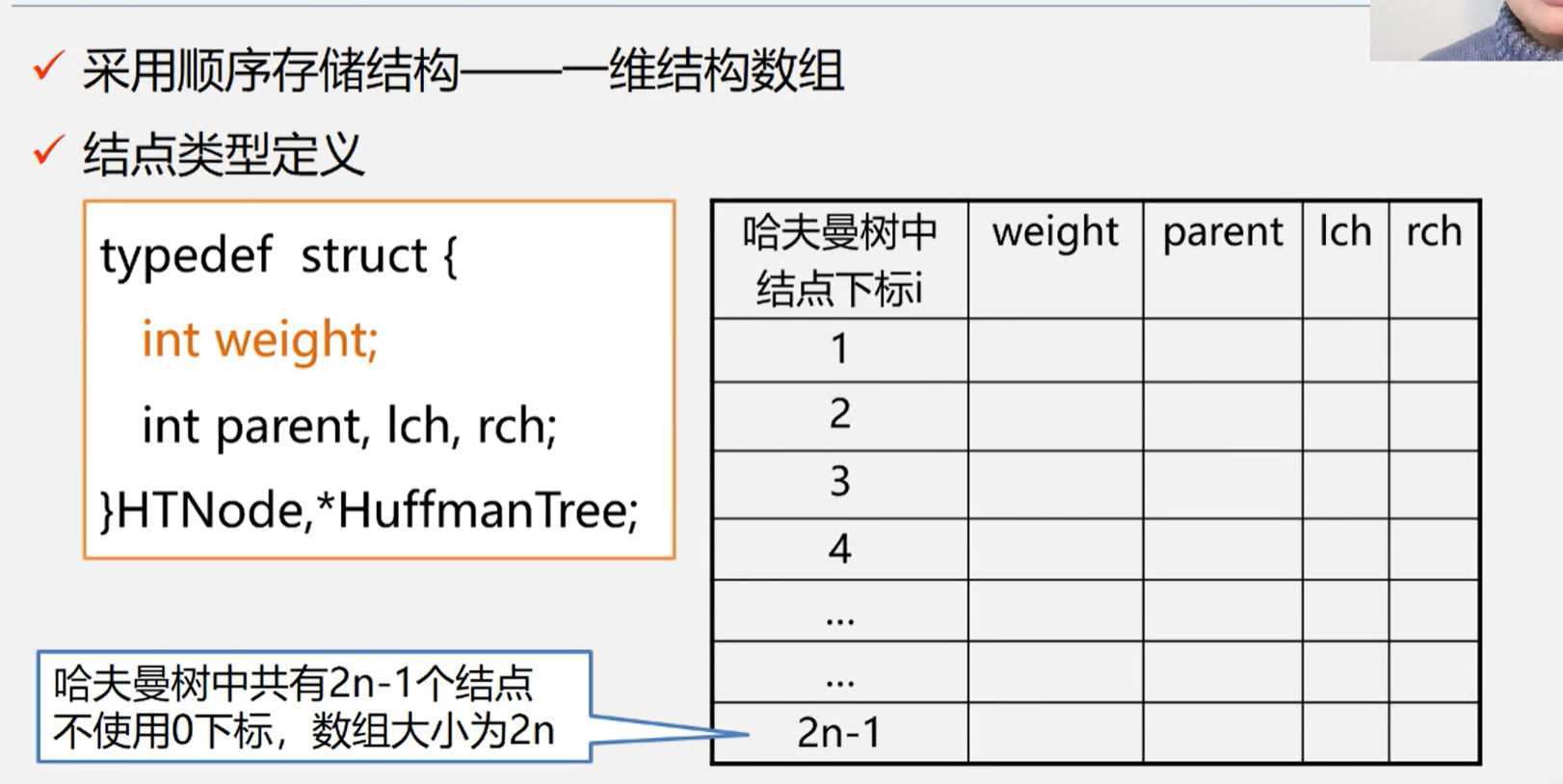
    注意重置min的过程，可以改进算法，但是作者还没有学到遍历，所以并没有采取其他方式

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    98
    99
    100
    101
    102
    #include "stdio.h"
    #include "stdlib.h"

    #define status int
    #define OK 1
    #define ERROR (-1)
    #define true 1
    #define false 0
    #define ElemType int
    #define MAXSIZE 30
    #define OVERFLOW (-1)
    #define CHUNKSIZE 80

    #include "stdio.h"
    #include "stdlib.h"

    typedef struct HTNode {
        int weight;
        int parent, lch, rch;
    } HTNode, *HuffmanTree;
    //采用双亲表示法，但是会记录左右孩子的位置

    void Select(HTNode *htNodes, int size, int *min1, int *min2) {
        //以下算法用于去出较次和最次的元素
        for (int i = 0; i < size; ++i) {
            if ((htNodes + i)->parent == 0
                && (htNodes + i)->weight < (htNodes + *min1)->weight) {//确保每小权的结点已经被选用

                *min2 = *min1;
                *min1 = i;
            } else if ((htNodes + i)->parent == 0
                       && (htNodes + i)->weight < (htNodes + *min2)->weight
                       && i != *min1) {

                *min2 = i;
            }
        }
    }

    void initMin(HTNode* htNodes,int size,int *min1,int *min2){
        //重置最小值，防止取出来的最小值是已经被选过的
        int i = 0;
        for (; i < size; ++i) {
            if((htNodes+i)->parent==0){
                *min1=i++;//break使得++i失效
                break;
            }
        }
        for(;i<size;++i){
            if((htNodes+i)->parent==0){
                *min2=i;
                break;
            }
        }
    }

    status creatNode(HTNode *htNodes, int *nums, int size) {
        int i = 0;
        int min1 = 0, min2 = 0;
        int size1;
        size1 = size * 2 - 1;
        //
        for (; i<size; ++i) {
            (htNodes + i)->weight = *(nums + i);
            (htNodes + i)->lch = 0;
            (htNodes + i)->rch = 0;
            (htNodes + i)->parent = 0;//一定要将parent重置为0
        }

        for (; i < size1 ; ++i) {
            initMin(htNodes,i,&min1,&min2);
            Select(htNodes, i, &min1, &min2);
            (htNodes + i)->weight = (htNodes + min1)->weight + (htNodes + min2)->weight;
            (htNodes + i)->lch = min1;
            (htNodes + i)->rch = min2;
            (htNodes + i)->parent = 0;
            (htNodes + min1)->parent = i;
            (htNodes + min2)->parent = i;
        }
    }

    int main() {
        int num;
        int nums[100] = {0};
        int tem;
        HTNode htNodes[100] = {0};//注意这里使用变量，不使用指针
        scanf("%d", &num);//num最大是5，因为，2n-1留一个0不用
    /*    if(num>5){
            printf("num too large");
            exit(-1);
        }*/
        for (int i = 0; i < num; ++i) {
            scanf("%d", &tem);
            nums[i] = tem;
        }
        creatNode(htNodes, nums, num);
        for (int i = 0; i < 2*num-1; ++i) {
            printf("%d ",htNodes[i].weight);
        }
        return 0;
    }

哈曼树的运用

哈夫曼编码

  1. 设计一种任意的编码都不是另一个编码的前缀

    如A(0)是B(00)的前缀

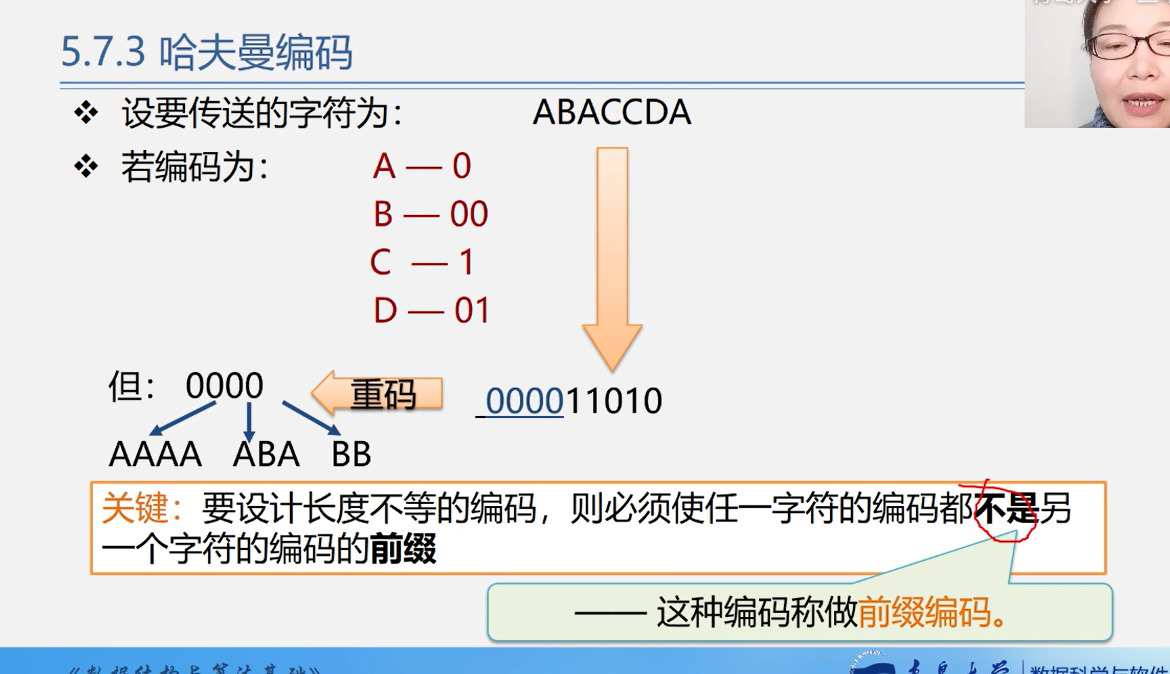
  2. 通过哈夫曼编码使得电文最短

    将要传输的字符出现的频率当作权值

  3. 问题

    • 为什么哈夫曼编码能确保不是前缀编码？

      因为每一个字符都是叶子结点，也就是说，没有哪个叶子是另个一个叶子的前缀，也就是没有相同的路径

    • 为什么哈夫曼树能确保字符编码总长最短？

      才用权的方式，权重大的离根节点更近，所以形成的编码最短。换句话说哈夫曼树的加权路径最短

  4. 性质

    • 哈夫曼编码是前缀码
    • 而且是最有前缀码
#数据结构和算法
树和二叉树
https://tsy244.github.io/2023/04/05/数据结构/树和二叉树/
Author
August Rosenberg
Posted on
April 5, 2023
Licensed under